Translation (exercice)

Bonjour de l'aide svp
[Ox) et [Oy) sont deux demi-droites.A et B sont fixes sur [Ox).Soit M et N des points variables sur [Oy) tels que MN =AB et N € [Ny). On pose P et Q les milieux respectifs de [AM] et [BN].
Prouver que Q est l'image de P par une translation indépendante de M et N
J'ai tracé la parallèle passant par A à (MN) mais j'ai pas trouvé d'idée
Merci vivement pour votre aide

@galois , bonjour,
Je regarde ton énoncé et quelque chose ne va pas.
Tu as écrit $N∈[Ny)N\in[Ny)$
Bien sûr, c'est vrai mais ça ne sert à rien...
J'ai admis $N∈[My)N\in[My)$
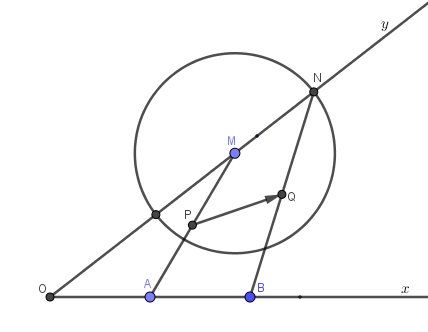
Vérifie si c'est ça .

Schéma
(le cercle sert seulement à la construction pour obtenir $M N = A B$ )

Piste,
Tu peux calculer $PQ→\overrightarrow{PQ}$ en fonction de $AB→\overrightarrow{AB}$ et $MN→\overrightarrow{MN}$ en utilisant deux fois la relation de Chasles
$PQ→=PA→+AB→+BQ→\overrightarrow{PQ}=\overrightarrow{PA}+\overrightarrow{AB}+\overrightarrow{BQ}$
$PQ→=PM→+MN→+NQ→\overrightarrow{PQ}=\overrightarrow{PM}+\overrightarrow{MN}+\overrightarrow{NQ}$

Tu ajoutes ces deux égalités, tu simplifies, tu divises par $2$ et tu obtiendras la relation souhaitée.

Ensuite, il faut que tu prouves que le vecteur $MN→\overrightarrow{MN}$ est constant quelles que soient les positions de M et N sur $[0 y)$ (en respectant évidemment les hypothèses)

Tu pourras ainsi le déduire la translation demandée.

Reposte si besoin.

@mtschoon merci vivement oui pour l'énoncé N €[My)
Le vecteur MN est constant puisque son sens sa direction et sa longueur AB sont fixes
C'est très gentil merci beaucoup

C'est bien @galois.
J'espère que tu as bien défini le vecteur de la translation .

@mtschoon oui je viens de trouver mercie

De rien @galois , c'est parfait si tu as trouvé.

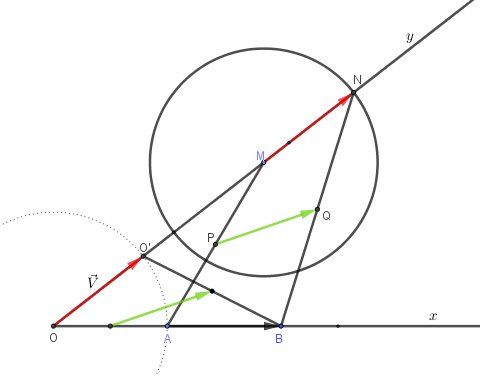
Une illustration possible,

Pour $M$ en $O$ , $N$ est en $O^{'}$
Soit $V→=OO′→\overrightarrow{V}=\overrightarrow{OO'}$
Le vecteur de la translation peut se noter $12(V→+AB→)\dfrac{1}{2}(\overrightarrow{V}+\overrightarrow{AB})$