Sujet Math expert Terminale

Bonjour,
Je suis bloquer sur un exercice et je ne sais vraiment pas comment le résoudre est-ce que vous pouvez m'aider s'il vous plaît:
Soit M une matrice carrée, non nul d'ordre n Tels que A+B=In
Soit M une matrice carrée d'ordre n telle qu'il existe de réel non nul est distinct, ¥ et u tels que: M=aA+uB et M^2=a^2A+u^2B
1_Montrer que (M-aIn)(M-uIn)=(M-uIn)(M-aIn)=0n
2_en déduire que AB=BA=0n et A^2=A et B^2=B
3_Demontrer que pour tout p qui appartient à N, on a M^p=a^pA+u^pB
Merci d'avance

Ce message a été supprimé !

@Sarah3075 , bonjour,

Il est très "calculatoire", ton exercice.
Si tu as besoin, je t'indique la marche globale pour faire les calculs.

Remarque :
Je simplifie les notations
$I_n=I$
$u = b$ pour harmoniser avec $a$
Les hypothèses sont donc :
$A + B = I$ , $M = a A + b B$ et $M^2=a^2A+b^2B$

Pistes,

1 ) Pour démontrer que $(M−aI)(M−bI)=O\boxed{(M-aI)(M-bI)=O}$
Tu développes et regroupes
$M-aI)(M-bI)=M^2-(a+b)M+abI$
Tu remplaces $M$ et M^2$ par les expressions données et après simplifications , tu dois arriver à
$- a b (A + B) + a b I = - a b I + a b I = O$
Même principe pour $(M−bI)(M−aI)=O\boxed{(M-bI)(M-aI)=O}$

2 )Tu utilises $(M - a I) (M - b I) = O$ dans laquelle tu remplaces $M$ par $a A + b B$ et $I$ par $A + B$
Après développement et simplification tu dois arriver $BA=O\boxed{BA=O}$
Même principe en partant de $(M - b I) (M - a I) = O$ , tu dois arriver à $AB=O\boxed{AB=O}$

En partant de $M^2=(aA+bB)^2$ et en développant, sachant que $A B = B A = O$ , tu dois arriver $M^2=a^2A^2+b^2B^2$
Vu que $M^2=a^2A+b^2B$ , tu peux déduire $A2=A\boxed{A^2=A}$ et $B2=B\boxed{B^2=B}$

3 ) Une petite récurrence toute simple convient.

Bons calculs et reposte si besoin.

@mtschoon merci beaucoup j’ai enfin réussi à finir l’exercice.J’ai juste une dernière questions d’application
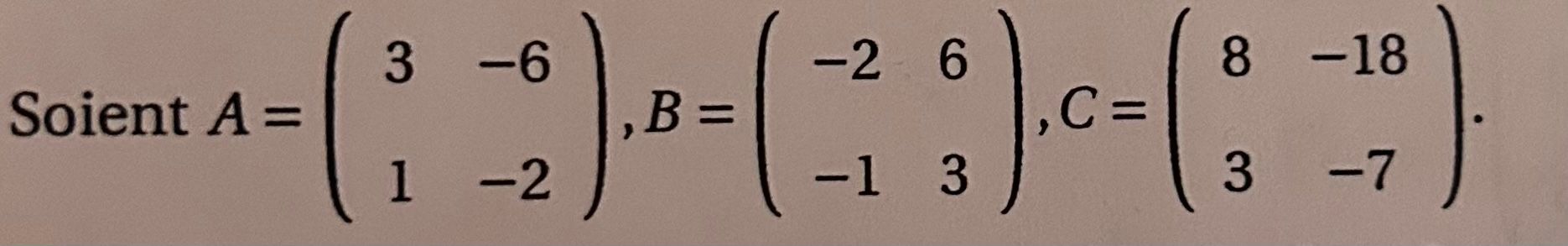
Avec c’est matrice il faut que je déduise pour tout p qui appartient à N,la matrice M^p.Pour cette question je n’est pas trop compris est ce que je dois juste remplacer M A et B par les matrice donner où est ce que je dois trouver M^p avec une vrais valeur.

C'est bien @Sarah3075 d'avoir traité tout l'exercice !

Pour l'application, je pense qu'il faut d'abord que tu choisisses les deux matrices parmi les 3 proposées pour lesquelles la somme vaut $I$ .
Tu calcules donc $A + C$ , $B + C$ , $A + B$ et tu conclus que $A$ et $B$ doivent être utilisées car $A + B = I$
Je suppose que tu dois faire le calcul de $M^p$ en utilisant la formule trouvée, en remplaçant $A$ et $B$ par leurs valeurs.

Tu dois obtenir, sauf erreur

$−2ap+3bp)M^p=\begin{pmatrix}3a^p-2b^p\ \ \ -6a^p+6b^p\cr a^p-b^p\ \ \ \ \ -2a^p+3b^p\end{pmatrix}$

Je ne vois pas quoi faire d'autre...