Bonjour, s'il vous plaît aidez moi à résoudre mon exercice sur la Bijection réciproque
-
HHermann1474 dernière édition par Hermann1474
f(x) = 1/(1-x²) et f est strictement croissante sur ] 0;1[.
Justifie que f réalise une bijection de]o ;1 [ sur un intervalle j, à déterminer.
-
mtschoon dernière édition par mtschoon

@Hermann1474 , bonjour,
Pense à la formule de politesse...
Si tu as étudié les variations de f pour x∈]0,1[x\in ]0,1[x∈]0,1[, tu as dû trouver que f est définie,continue, dérivable et strictement croissante de ]0,1[]0,1[]0,1[ vers ]1,+∞[]1,+\infty[]1,+∞[
Donc, tout élément de ]0,1[]0,1[]0,1[ a une image (forcément unique) dans ]1,+∞[]1,+\infty[]1,+∞[ et tout élément de ]1,+∞[]1,+\infty[]1,+∞[ a un antécédent unique dans ]0,1[]0,1[]0,1[
J=]1,+∞[J= ]1,+\infty[J=]1,+∞[
donc f réalise une bijection de ]0,1[]0,1[]0,1[ vers ]1,+∞[]1,+\infty[]1,+∞[
fff a donc une bijection réciproque f−1f^{-1}f−1 de ]1,+∞[]1,+\infty[]1,+∞[ vers ]0,1[]0,1[]0,1[Piste pour le calcul de f−1(x)f^{-1}(x)f−1(x)
f−1(x)=yf^{-1}(x)=yf−1(x)=y <=> x=f(y)x=f(y)x=f(y) <=> x=11−y2x=\dfrac{1}{1-y^2}x=1−y21Tu calcules yyy en fonction de xxx.
Donne ta réponse si tu souhaites une vérification.
-
HHermann1474 dernière édition par
Excusez pour ma maladresse
Pour résoudre l'exercice
Dertemino's l'ensemble de définition
f(x) =1/(1-x²)
Df= R{-1;1}
Limites aux bornes de Df
Lim f(x) =lim (1/(1-x²))
x->-00
=0
Lim f(x) = lim (1/(1-x²))
x->+00
=0
-
mtschoon dernière édition par mtschoon

Ce n'est pas Df qu'il faut utiliser mais seulement ]0,1[]0,1[]0,1[ comme te l'indique l'énoncé.
Les limites à chercher sont :
lorsque xxx tend vers 000 ( par valeurs supérieures à 000) et lorsque xxx tend vers 111 (par valeurs inférieures à 111)Tu pourras faire ensuite le tableau de variations de fff pour x∈]0,1[x\in]0,1[x∈]0,1[
-
mtschoon dernière édition par mtschoon

@Hermann1474 , voilà ce que tu dois trouver, après calculs, comme tableau de variations de fff pour x∈]0,1[x\in ]0,1[x∈]0,1[
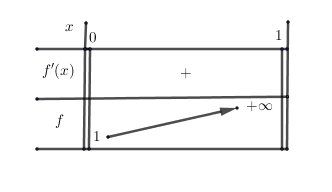
Reposte si besoin.