Application, calcul d'image avec intervalle [ Besoin aide ] et merci d'avance

On considère l’application f : R → R, x --> x²

Déterminer f(R), f([1, 2]), f([−2, 0[ ) et f( ] − 2, 1[ ).

Bonjour j'aurais besoin d'aide, plus précisément des vérifications :
alors F(R) je sais pas du tout comment le calculer donc si quelqu'un pourrait me montrer le calcul, (c'est pour un oral).
Pour les autres je l'ai fait mais j'aurais besoin de savoir si c'est bon pour pas paraitre débile à l'oral :lol:
PS : Je sais c'est peut être facile mais j'ai l'impression de faire ou d'avoir fait de la merde
f([1, 2]) = [1;4]
f([−2, 0[ ) = [-4;0[
f( ] − 2, 1[ ) = ]-4;1[

@Robz Bonsoir,

Un carré est toujours positif, vérifie tes réponses.

Bonjour,

@Robz je te conseille de construire la parabole d'équation $y=x^2$
IL te sufira de regarder les abscisses et ordonnées des points utiles pour trouver les réponses.
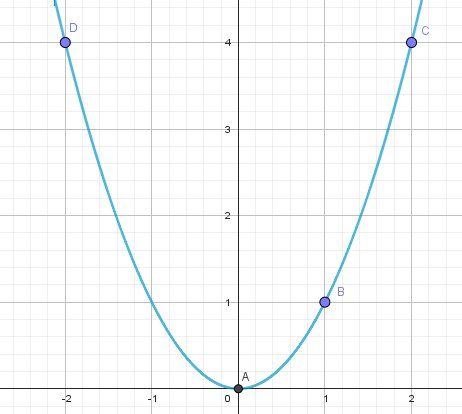
paraboley=x^2.jpg

Pour x variant de $−∞-\infty$ à $+∞+\infty$ , les ordonnées des points de la parabole varient de $0$ et $+∞+\infty$
$f(R)=[0,+∞[f(R)=[0,+\infty[$
Tu peux écrire $f(R)=R^{+}$

Ta réponse pour $f ([1, 2])$ est exacte.

Ta réponse pour $f ([- 2, 0 [)$ est à revoir.

Ta réponse pour $f (] - 2, 1 [)$ est à revoir.

Revois tes réponses et donne les , si tu souhaites une vérification.

Bonjour, merci de m'avoir accorder un peu de temps, je me suis corrigé du coup normalement tout est bon :
f([1, 2]) = [1;4]
f([−2, 0[ ) = ]0,4]
f( ] − 2, 1[ ) = ]0,4[
f(R) = R+

@Robz

La troisième réponse est à vérifier.

Bonjour,

@Robz , comme te l'a dit @Noemi , revois la troisième réponse : problème de crochet.