Equations Complexes : exposant

Bonjour, j'ai une question, peut-être un peu bête, qui me tourmente.
Par exemple, pour z^3 = 64, si on supprime les puissances de 3 de chaque coté, on trouve une seul réponse z = 4, il manque donc les 2 autres réponses complexes.

Cependant pour la résolution de l'équation
( x^2 + 4x + 1 )^2 + ( 3x + 5 )^2 = 0, la correction est la suivante :
( x^2 + 4x + 1 )^2 + ( 3x + 5 )^2 = 0
<=> ( x^2 + 4x + 1 )^2 = i^2( 3x + 5 )^2
<=> ( x^2 + 4x + 1 ) = +/- i(3x + 5)
Et puis on fais passer tout d'un coté et on résout les 2 équations du second degré, mais en supprimant les exposant, on ne risque pas de louper des réponses complexes ?

Je vous remercie d'avance de votre réponse.

@OKiDoK Bonsoir,

Pour $z^3=64$ , si tu supprimes les puissances, tu trouves une solution $z = 4$
soit $z^3-64= (z-4)(z^2+4z+16)$
la factorisation te permet de trouver les autres racines.

Pour la résolution de $x^2+4x+1)^2-i^2(3x+5)^2= 0$ tu utilises l'identité remarquable : a^2-b^2= (a-b)(a+b)
l'équation devient :
$x^2+4x+1)-i(3x+5)][(x^2+4x+1)+i(3x+5)]=0$

On a ici encore factorisé donc pas de possibilité d'oublier des réponses.

Ah d'accord, je vous remercie pour cette réponse claire et précise.

Bonsoir,

Autre méthode possible en utilisant la forme exponentielle

$z^3=64$ <=> $z^3=4^3$

Soit $^{i\theta}$

L'équation sécrit : $r3e3iθ=43e0ir^3e^{3i\theta}=4^3e^{0i}$

d'où :
$r^3=4^3$ <=> $r = 4$
$3θ=0+2kπ3\theta=0+2k\pi$ <=> $θ=2kπ3\theta =\dfrac{2k\pi}{3}$ avec $k∈Zk\in Z$

donc :
$z=4e2kiπ3\boxed{z=4e^{\dfrac{2ki\pi}{3}}}$ avec $k∈Zk\in Z$

Conclusion : 3 solutions ( les racines cubiques de 64)

Pour $k = 0$ : $z = 4$
Pour $k = 1$ : $z=4e2iπ3z=4e^{\dfrac{2i\pi}{3}}$
Pour $k = 2$ : $z=4e4iπ3z=4e^{\dfrac{4i\pi}{3}}$

On peut bien sur mettre ces solutions sous forme algébrique.

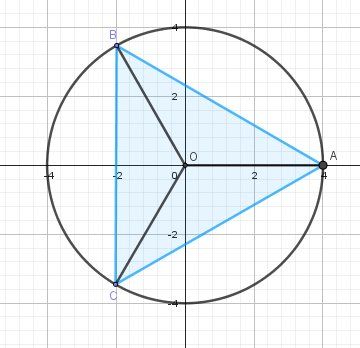
Illustration graphique dans le plan complexe.

$z_A=4$
$zB=4e2iπ3=−2+2i3z_B=4e^{\dfrac{2i\pi}{3}}=-2+2i\sqrt 3$
$zC=4e4iπ3=−2−2i3z_C=4e^{\dfrac{4i\pi}{3}}=-2-2i\sqrt 3$