Résolution d'une simple inéquation
-
Wakala Waka dernière édition par
Bonjour à tous, j'ai simplement besoin d'isoler I dans cette inéquation, ce que je n'arrive pas à faire étant très nul.
Merci d'avance, pour vos aides éventuelles !
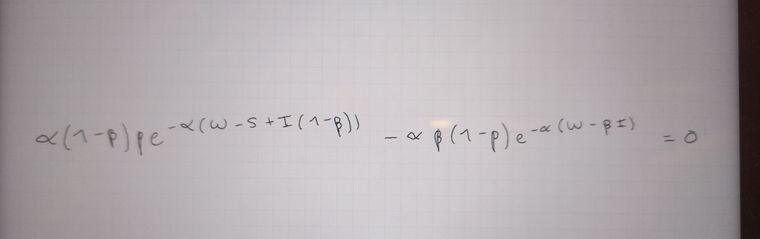
-
@Wakala-Waka Bonsoir,
Tu veux isoler quelle variable ?
Utilise la factorisation pour résoudre l'équation.
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Pour autant que j'aie bien lu l'énoncé :
Ce n'est pas une inéquation ...
α∗(1−β)∗p∗e−α∗(ω−S+I(1−β))−α∗β∗(1−p)∗e−α∗(ω−β∗I)=0\alpha*(1 - \beta) * p * e^{-\alpha * (\omega - S+I(1-\beta))} - \alpha * \beta * (1-p) * e^{-\alpha *(\omega - \beta * I)} = 0 α∗(1−β)∗p∗e−α∗(ω−S+I(1−β))−α∗β∗(1−p)∗e−α∗(ω−β∗I)=0
α∗(1−β)∗p∗e−α∗(ω−S+I(1−β))=α∗β∗(1−p)∗e−α∗(ω−β∗I)\alpha*(1 - \beta) * p * e^{-\alpha * (\omega - S+I(1-\beta))} = \alpha * \beta * (1-p) * e^{-\alpha *(\omega - \beta * I)} α∗(1−β)∗p∗e−α∗(ω−S+I(1−β))=α∗β∗(1−p)∗e−α∗(ω−β∗I)
α∗(1−β)∗p∗e−αω∗eαS∗e−αI∗eαβI=α∗β∗(1−p)∗e−αω∗eαβI\alpha*(1 - \beta) * p * e^{-\alpha \omega} * e^{\alpha S} * e^{-\alpha I} * e^{\alpha \beta I} = \alpha * \beta * (1-p) * e^{-\alpha \omega} * e^{\alpha \beta I}α∗(1−β)∗p∗e−αω∗eαS∗e−αI∗eαβI=α∗β∗(1−p)∗e−αω∗eαβI
Si alpha est non nul :
(1−β)∗p∗eαS∗e−αI=β∗(1−p)(1 - \beta) * p * e^{\alpha S} * e^{-\alpha I} = \beta * (1-p) (1−β)∗p∗eαS∗e−αI=β∗(1−p)
Si beta non nul et p différent de 1, il vient :
eαI=(1−β)∗p∗eαSβ∗(1−p)e^{\alpha I} = \frac{(1 - \beta) * p * e^{\alpha S} }{\beta * (1-p)} eαI=β∗(1−p)(1−β)∗p∗eαS
αI=ln((1−β)∗p∗eαSβ∗(1−p))\alpha I = ln( \frac{(1 - \beta) * p * e^{\alpha S} }{\beta * (1-p)})αI=ln(β∗(1−p)(1−β)∗p∗eαS)
I=1α∗ln((1−β)∗p∗eαSβ∗(1−p))I = \frac{1}{\alpha} * ln( \frac{(1 - \beta) * p * e^{\alpha S} }{\beta * (1-p)})I=α1∗ln(β∗(1−p)(1−β)∗p∗eαS) ... si existe
Je n'ai rien relu ... et donc tu as fortement intérêt à vérifier.