Courbe Excel log normale inverse

Bonjour, j'ai réalisé une courbe log normale inverse sur excel. J'aimerais trouver la moyenne et l'écart type pouvait pour m'aider s'il vous plait merci beaucoup

@Tulipe003 , bonjour,

Ta question ne me semble est pas être postée dans la bonne rubrique vu que tu parles de Excel.
Elle aurait été mieux dans la rubrique Math-Outils

Je te mets un lien qui propose "Besoin d'aide"
*En posant ta question, tu devrais pouvoir obtenir une indication .

https://support.microsoft.com/fr-fr/office/loi-lognormale-inverse-fonction-0bd7631a-2725-482b-afb4-de23df77acfe

@mtschoon merci beaucoup pour votre lien! Mais cela ne répond pas vraiment à ma question j’ai bien rentré les paramètres ds la formule qui m’étaient donnés, j’obtiens ma courbe type courbe d’henry et on me demande de trouver la moyenne et l’écart type

Désolée @Tulipe003 , mais comme je te l'ai indiqué, il est possible de poser ta question en bas du lien que je t'ai indiqué. Fais le.

A tout hasard, vu que tu parles maintenant du type Henry , je te mets un lien sur la "droite de Henry".
https://www.techno-science.net/definition/5951.html

Bonnes recherches !

@Tulipe003 Bonjour,

A partir de quelles données travailles-tu ?

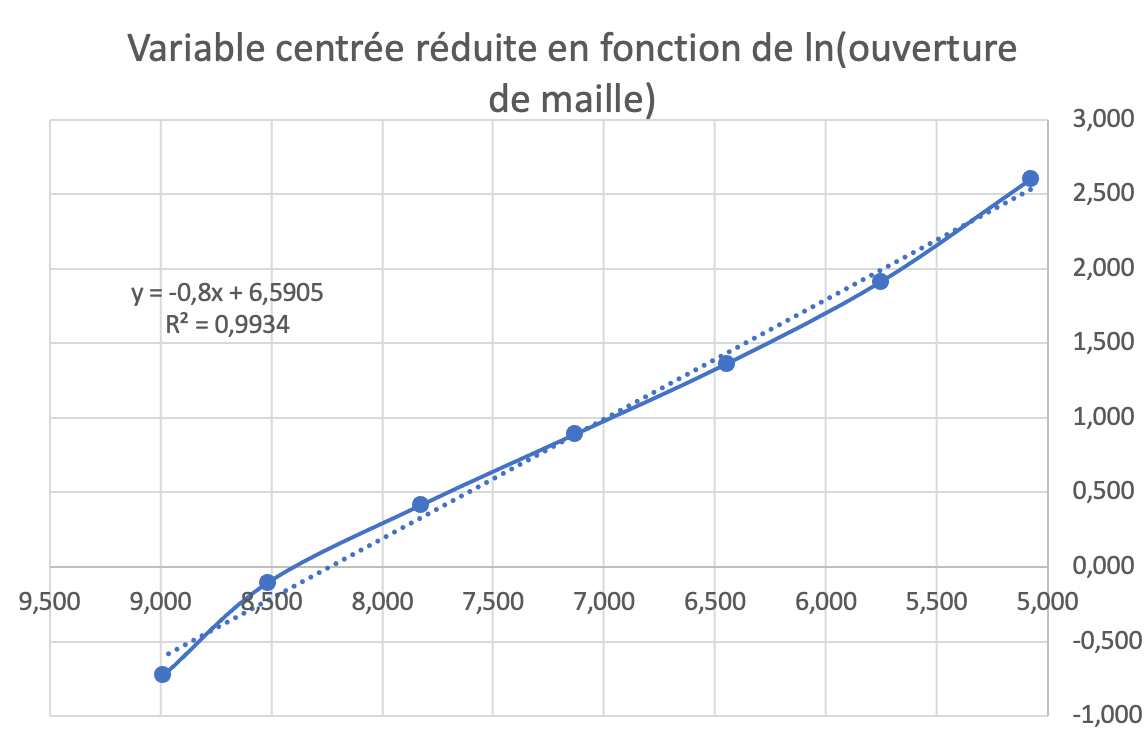
J'étudie la granulométrie de particules. J'ai donc en abscisse ln(ouverture de maille) et en ordonné la variable centrée réduite (log.normale.inverse) du refus relatif cumulé. La question qui m'est posée est de déterminer la moyenne et l'écart de type de cette granulométrie grâce à la courbe que j'ai mis en annexe

@Tulipe003 ,bonjour,

C'est bien d'avoir donner ton schéma.

Je te livre quelques réflexions mathématiques relatives à ce schéma.

Quand tu dis "trouver la moyenne et l’écart type" on ne sait pas toujours pas de quelle variable tu parles...
J'imagine qu'il s'agit de $Y$ (? ? ?)

La fonction affine $Y = - 0.8 X + 6.5905$ (droite de régression linéaire de $Y$ en $X$ ) est décroissante ( les abscisses sont orientées dans le sens inhabituel, mais ça ne change rien).

Donc $R$ (coefficient de corrélation linéaire) est négatif ( il est forcément compris entre -1 et 0)
$R=−R2R=-\sqrt{R^2}$
$R≈−0.99967R\approx -0.99967$
Vu que $R$ est très voisin de -1, la corrélation linéaire entre Y et X est très forte donc cette relation
$Y = - 0.8 X + 6.5905$ est utilisable.

Que connais tu ?

Si tu connais $Xˉ\bar{X}$ ( moyenne de $X$ ) et $σ(X)\sigma(X)$ (écart-type de $X$ ), tu peux, avec cette relation, trouver $Yˉ\bar{Y}$ (moyenne de $Y$ ) et $σ(Y)\sigma(Y)$ (écart-type de Y)

Si c'est ce que tu cherches ( ? ? ? ) , je te mets les formules, sachant que $V(X)=(σ(X))2V(X)=(\sigma(X))^2$ et $V(Y)=(σ(X))2V(Y)=(\sigma(X))^2$

$Y=aX+b\boxed{Y=aX+b}$
d'où
$Yˉ=aXˉ+b\boxed{\bar{Y}=a\bar{X}+b}$ ici : $Yˉ=−0.8Xˉ+6.5905\bar{Y}=-0.8\bar{X}+6.5905$

$V(Y)=a2V(X)\boxed{V(Y)=a^2V(X)}$ ici : $V(Y)=(-0.8)^2V(X)$
c'est à dire $V(X)V(Y)=0.64\ V(X)$
c'est à dire $σ(X)\sigma(Y)=0.8\ \sigma(X)$

C'est tout ce que je peux dire et désolée si ce n'est pas ce que tu cherches...

Dans excel j'ai dû rentrer: =LOI.NORMALE.INVERSE.N(cellule;0;1) qui correspond à =LOI.NORMALE.INVERSE.N(probabilité;espérance;écart-type)