Géométrie dans l’espace
-
Llalie123 dernière édition par
Bonjour,
je n’arrive pas à résoudre cet exercice et il possible d’avoir de l’aide.
Merci d’avance.
Sujet: ABCDEFGH est un cube, M est un point de [EF], N de [GH] et P de [AD].- Déterminer l'intersection des plans (MNP) et (EFG).
En déduire l'intersection des plans (MNP) et (ABC) , puis des plans (MNP) et (DCG) - Justifier que les droites (MN) et (EH) sont sécantes. En déduire l'intersection des plans (MNP) et (ADH) , puis des plans (MNP) et (ABF).
- Déterminer et construire ainsi la section du cube par le plan (MNP) .
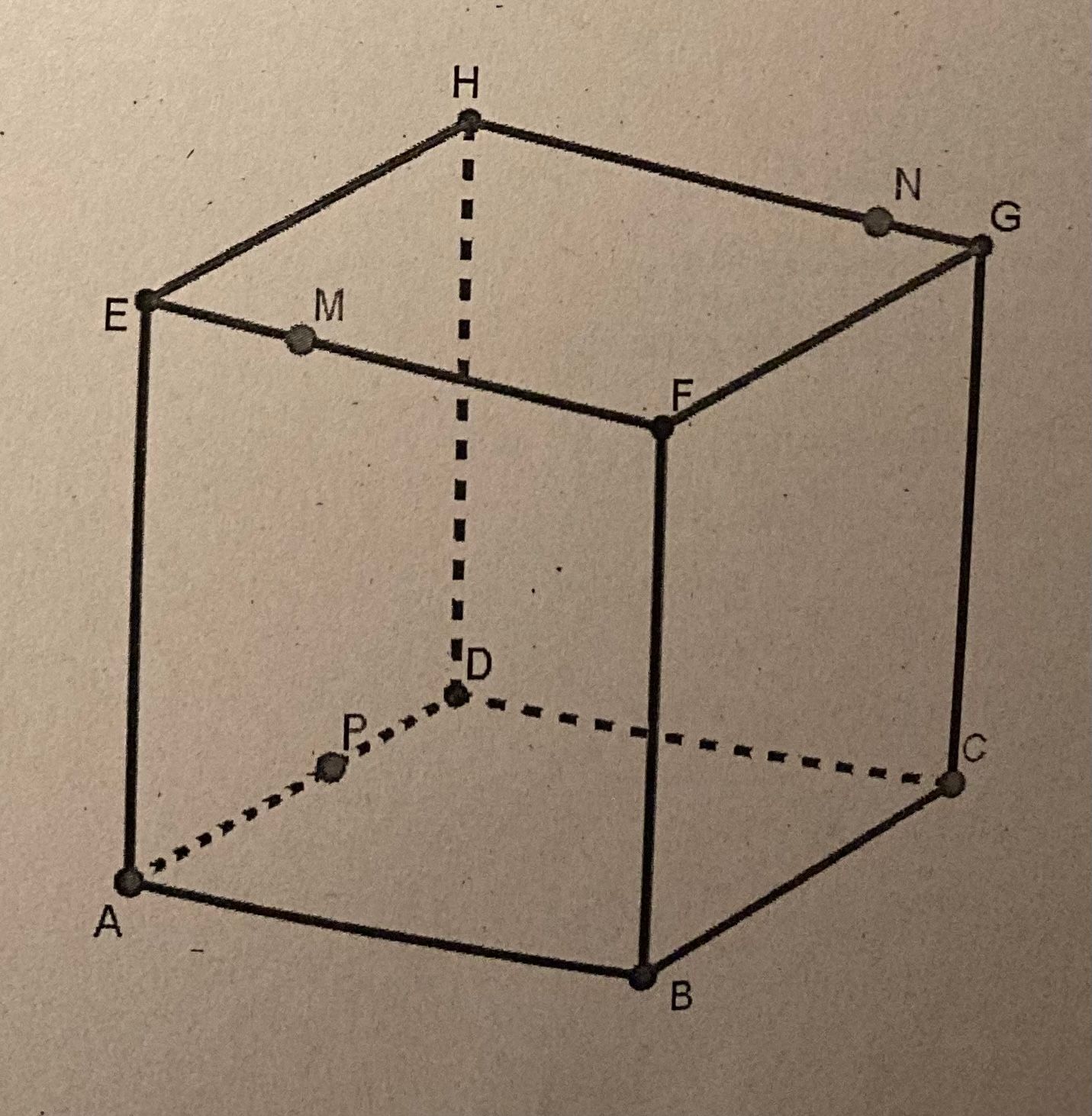
- Déterminer l'intersection des plans (MNP) et (EFG).
-
mtschoon dernière édition par mtschoon

@lalie123, bonjour,
J'ai essayé de compléter le cube avec les éléments nécessaires pour répondre aux questions posées.
La droite (Δ)(\Delta)(Δ) est la droite parallèle à (MN) passant par PPP
Elle coupe (DC)(DC)(DC) en QQQ
RRR est le point d'intersection de (EH)(EH)(EH) avec (MN)(MN)(MN)
SSS est le point d'intersection de (PQ)(PQ)(PQ) avec (AB)(AB)(AB)
TTT est le point d'intersection (RP)(RP)(RP) avec (MS)MS)MS) et il se trouve sur (EA)(EA)(EA)
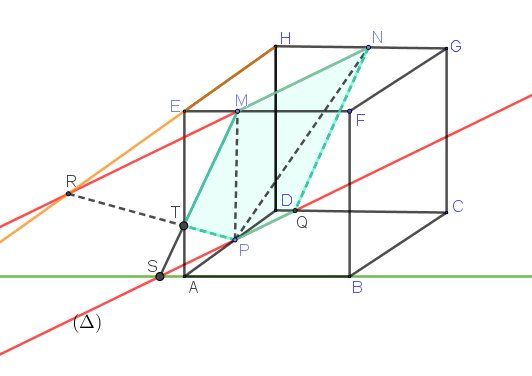
Donne tes réponses pour vérification si tu le souhaites.
-
Llalie123 dernière édition par
@mtschoon
Merci beaucoup j’ai réussi l’exercice !
Bonne journée
-
mtschoon dernière édition par

De rien @lalie123 et bon week-end à toi.