Triangle isocèle, mesure d'un angle, barycentre
-
TTenin camara dernière édition par Noemi
Bonjour j'ai besoin d'aide à propos d'un exercice de maths voici l'énoncé: soit ABC un triangle isocèle telque:BC= 2 ; AB=AC=3 . On désigne par A' le milieu du segment [BC] et H l'orthocentre de ABC .1*) Démontrer par deux méthodes différentes que : cosBÂC =7/9
2*) Soit BC le projeté orthogonal de B sur la droite AC
a) calculer le rapport :B'A/B'C
b) Déterminer deux nombres a et c tels N' est le barycentre des points pondérées (A,a); (C;c) pr deux méthodes différentes
3) En déduire trois nombres a;b;et c tels que H est le barycentre des points pondérées (A;a) , (B;b) et (C;c)
Je vous remercie d'avance
-
mtschoon dernière édition par mtschoon

Je mets un schéma pour plus de clarté.
(les cercles en pointillés sont là seulement pour la construction)
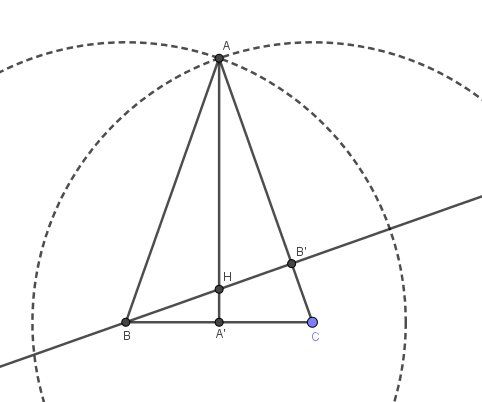
-
mtschoon dernière édition par

@Tenin-camara , piste pour démarrer,
Je ne sais pas où tu en es dans ton cours...
1 ) Formule d'al-Kashi si tu connais
a2=b2+c2−2bc cosBAC^a^2=b^2+c^2-2bc\ cos\widehat {BAC}a2=b2+c2−2bc cosBAC
a=2,b=c=3a=2, b=c=3a=2,b=c=3
Tu dois trouver, sauf erreur, cosBAC^=79\boxed{cos\widehat {BAC}=\dfrac{7}{9}}cosBAC=97
L'énoncé te demande une autre façon.
Par exemple,
cosA′AC^=AA′ACcos\widehat{A'AC}=\dfrac{AA'}{AC}cosA′AC=ACAA′
AC=3AC=3AC=3
Avec le théorème de Pythagore, tu trouvesAA′=8AA'=\sqrt 8AA′=8
Ainsi cosA′AC^=83cos\widehat{A'AC}=\dfrac{\sqrt 8}{3}cosA′AC=38Avec une formule de duplication :
cosBAC^=2cos2(cosA′AC^)−1=2(89)−1=79cos\widehat {BAC}=2cos^2(cos\widehat{A'AC})-1=2(\dfrac{8}{9})-1=\boxed{\dfrac{7}{9}}cosBAC=2cos2(cosA′AC)−1=2(98)−1=97Pour la 2) relis ton énoncé
Tu as écris "Soit BC le projeté orthogonal de B sur la droite AC"
Cela ne veut rien dire...je suppose qu'il s'agit du point B′B'B′Essaie de poursuivre.