Probabilites cercle trigonometrique

Bonjour,

Je viens de créer mon premier compte sur un forum de math car depuis une semaine je bloque sur un exo que j'arrive pas a résoudre. Je n'ai aucune idee comment trouver X
Voici l'exo

On lance une bille dans la roulette a 16 cases correspondant au nombres remarquables.

Le gain initial est de 0€. Si le gain final est positif on repart avec de l’argent, si
il est négatif on doit de l’argent au casino.
Si le cosinus de la case est une fraction dont le dénominateur est 2 on ajoute 1
au gain initial sinon on soustraie 1 au gain initial.
Puis si le sinus de la case est une fraction dont le dénominateur est 2 on ajoute
1 au gain sinon on soustrait 1 au gain.
Puis si le cosinus est strictement positif on multiplie le gain par -1, sinon on le
multiplie par 1.
Puis si le sinus est strictement positif on multiplie le gain par 1, sinon par -1
Si le cosinus et le sinus sont nuls en même temps, on oublie les règles précé-
dentes et on repart instantanément avec 1000€
On note U le nombre de tours qu’elle fait. On modélise U par une v.a. équi-répartie sur {1, . . . , 100}. On note C le cadrant de la bille que l’on représente par une v.a. équirépartie sur {0, π/2 , π, 3π/2 }.. On note θ la v.a. équi-répartie à valeur dans {0, π/6 , π/4 , π/3 }. Toutes les variables aléatoires précédentes sont Indépendantes. On note X le gain final en euros du joueur
Montrer que P(X = 1000) = 0.
Exprimer X en fonction de U,C et θ.
Donner la loi de X.
Calculer l’espérance de X.
Calculer la variance de X.
Si on répète l’expérience 4 fois de façon indépendante, quelle est la probabilité
que l’on ait gagné 8 euros.

Pour le 1 je sait qu'ils sont disjoncts donc impossible d'avoir cos et sin = 0 en meme temps mais pour trouver X?
Je vous remercieeme temps mais pour trouver X?
Je vous remercie

Bonjour,
Je reviens vers vous pour vérifier mon hypothèse

Exprimer X en fonction de U,C et θ
U= les tours
C= les quadrans qui vont donner le signe *(+1 )ou (-1 )
θ= les valeurs
donc θ sin et cos avec valeurs avec dénominateurs 2
Dans chaque cadran on a 6 valeurs avec dénominateur 2 (3 valeurs sin et 3 valeurs cos)
Alors on a X=U(Cθ)
Si on a 16 case en total a priori on doit diviser par 16 posibilites. Si on a pour sin 12 valeurs avec denominateur 2 et pour cos 12 valeurs avec denominateur 2, alors dans 12/16 case an vas gagner 1€+1€ et dans 4/16 on vas perdre (-1)+(-1) puis le C intervient pour trouver le signe!?
Je n'arrive pas a exprimer mathématiquement sin et cos en même temps. Je croit que je doit utiliser les probabilités conditionnelles, mais comment exprimer ensemble le sin et cos?
Merci beaucoup pour vos reponses

Bonjour

Les 16 "nombres remarquables" sont, je présume :

0 , Pi/6 , Pi/4 , Pi/3 , Pi/2 , 2Pi/3 , 3Pi/4 , 5Pi/6 , Pi , 7Pi/6 , 5Pi/4 , 4Pi/3, 3Pi/2 , 5Pi/3 , 7Pi/4 , 11Pi/6

Pour moi, il n'y a déjà pas consensus pour savoir dans quel quadrant sont certains de ces nombres remarquables.

Exemple :

Pi/2 est-il :

a) dans le 1er quadrant uniquement.
b) dans le 2ème quadrant uniquement
c) à la fois dans le 1er et dans le 2ème quadrant
d) A la limite des 1er et 2ème quadrant et ne fait partie d'aucun de ces quadrants.

Cela me semble déjà ennuyeux (rien qu'un peu) pour déterminer la variable C

Je présume (pas clair dans l'énoncé) que :
C = 1 pour un angle compris dans [0 ; Pi/2]
C = 2 pour un angle compris dans [Pi/2 ; Pi]
C = 3 ...
C = 4 ...

Ou alors la variable C est la valeur de l'angle ????

Je ne suis pas sûr non plus de bien comprendre la définition de Theta dans l'énoncé.
Peut être l'angle mesuré à partir du début du quadrant où la bille se trouve et la position exacte de la bille ?
Mais sans que cela soit écrit dans l'énoncé ... ???

@Black-Jack
Bonjour,
L'enonce est

On va considérer un jeu de casino très particulier : une roulette trigonométrique. Le
concept est le suivant : Il y a 16 cases correspondants aux angles remarquables du
cercle trigonométrique. Les règles sont les suivantes :

Le gain initial est de 0€. Si le gain final est positif on repart avec de l’argent, si
il est négatif on doit de l’argent au casino.
Si le cosinus de la case est une fraction dont le dénominateur est 2 on ajoute 1
au gain initial sinon on soustraie 1 au gain initial.
Puis si le sinus de la case est une fraction dont le dénominateur est 2 on ajoute
1 au gain sinon on soustrait 1 au gain.
Puis si le cosinus est strictement positif on multiplie le gain par -1, sinon on le
multiplie par 1.
Puis si le sinus est strictement positif on multiplie le gain par 1, sinon par -1
Si le cosinus et le sinus sont nuls en même temps, on oublie les règles précé-
dentes et on repart instantanément avec 1000€
On lance une bille dans la roulette. On note U le nombre de tours qu’elle fait. On
modélise U par une v.a. équirépartie sur {1, . . . , 100}. On note C le cadrant de la bille
que l’on représente par une v.a. équirépartie sur {0, π/2 , π, 3π/2 }.. On note θ la v.a. équi-répartie à valeur dans {0, π/6 , π/4 , π/3 }. Toutes les variables aléatoires précédentes sont indépendantes. On note X le gain final en euros du joueur.
Montrer que P(X = 1000) = 0.
Exprimer X en fonction de U,C et θ.
Donner la loi de X.
Calculer l’espérance de X.
Calculer la variance de X.
Si on répète l’expérience 4 fois de façon indépendante, quelle est la probabilité
que l’on ait gagné 8 euros.

@Black-Jack
Je suis d'accord avec le C qui represente le cadran et donc Theta est inclus dans C
Si Theta⊂ C alors p(Theta) ≤p(C)
En effet : C = Theta ∪(Theta\C). Or Theta et C\Theta sont
incompatibles. (C\Theta est l’ensemble des éléments de C qui ne sont pas éléments de A).
Donc : p(C) = p(Theta) + p(C\Theta)

ET puis pour calculer les probabilites dans Theta
Si deux événements sont dépendants plutôt qu’indépendants, comment calculer la
probabilité que les deux se réalisent, puisque la probabilité de réalisation de l’un dépend de la réalisation de l’autre?
Doit on utiliser les probabilites conditionnelles
p(Thetasin /saufThetacos) = p( Thetasin∩ Thetacos)/p(Thetasin) ?
Merci

@Black-Jack
C = 1 pour un angle compris dans [0 ; Pi/2]
C = 2 pour un angle compris dans [Pi/2 ; Pi]
C = 3 ...
C = 4
J'ai pense la meme chose!
Puis dans la C je suppose qu'est inclus Theta (sin et cos) donc,
(X=2)=C1=P(3/4)
puis dans le C1 sin + on a *1 et cos+ *(-1) qui font -
Donc
Dans le C1 on a P(X= - 2)= 3/4 ?

@Ella a dit dans Probabilites cercle trigonometrique :

Montrer que P(X = 1000) = 0

Rebonjour,

Mon avis sur cet énoncé.

Il est extrêmement mal écrit.
Outre les remarques déjà faite sur les interprétations déjà mentionnées ...

Comment interpréter par exemple :
"Si le cosinus de la case est une fraction dont le dénominateur est 2 ..."

Qu'est ce qu'on entend par le mot fraction.
Par exemple est ce que $22\frac{\sqrt{2}}{2}$ doit être compris comme une fraction de dénominateur 2 ? ... même si ce n'est pas une fraction dite "irréductible"

Pourquoi alors ne pas écrire 1 comme la fraction $22\frac{2}{2}$

Bref, il y a seulement 2 fractions irréductibles (pour les valeurs de sinus et cosinus) qui sont -1/2 et 1/2

Doit-on ne prendre ces 2 valeurs comme fractions avec dénominateur égal à 2 ...
ou faut-il aussi prendre comme fractions avec dénominateur égal à 2, les autres fractions qui ne sont pas irréductibles (comme -V2/2 , V2/2, -V3/2, V3/2)
... et pourquoi alors ne pas prendre aussi la valeur 2/2 ?

Si un des intervenants habituels du site (Noemi ou mtschoon ou ...) a un avis éclairé qui lèverait ce que je juge être des imprécisions (pour être gentil) de cet énoncé, je le lirai volontiers.

@Black-Jack
Bonjour,
J'ai pris les valeurs du (cos et sin) de Theta qui est inclus dans C et on se retrouve avec 32 posibilites......
Peut-être que on doit calculer P(U* cos (Theta inclus dans C)+ (U *sin(Theta inclus dans C)) / U
Moi j'ai pris toutes les valeurs du sin et cos de 16 angles j'ai fat un dessin mai j'arive pas a exprimer mathematiquement le sin et cos en meme temps
Theta inclus dans C1
0< =Theta<pi/2
0< 0;1;V3/2;1/2;V2/2;V2/2;1/2;V3/2 <PI/2
puis
Theta inclus dans C2
PI/2<= Theta<pi
.......... etc
P
Dans C1
P(X=2)= 6/8 P(X=-2)=2/8
j'ai fait ca pour chaque cadran mais j'ai un souci avec les donnes suivantes!
Puis si le cosinus est strictement positif on multiplie le gain par -1, sinon on le
multiplie par 1.
Puis si le sinus est strictement positif on multiplie le gain par 1, sinon par -1
Je ne sait pas si c'est bien!
Merci

Bonjour,

J'aurais tendance à faire quelque chose comme suit :

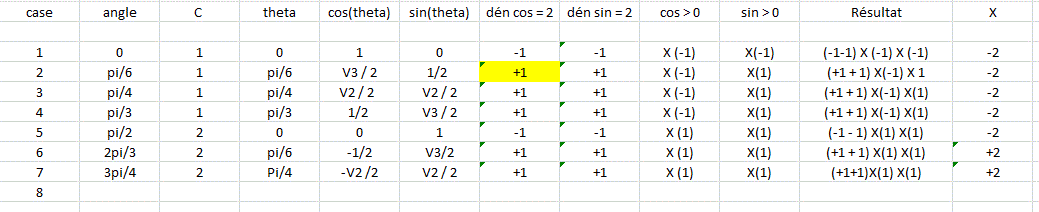
Sans titre.png

Et remplir évidemment pour les 36 cases ...

Attention, j'ai débuté le tableau en vitesse et je n'ai rien vérifié ...

@Black-Jack
Bonsoir,
J'ai fait la même chose dans un cercle trigonométrique

Mais transformer tout ça en probabilités ! Je trouve fou ce problème en classe de première!!!
Peut-etre que je dirait que la P(X= -2€ )= et P(X= 2€)=

Je vous remercie pour votre aide!