exercice trigonométrie
-
NNoah.s dernière édition par
Bonjour pourriez vous m'aider Merci
énoncé:
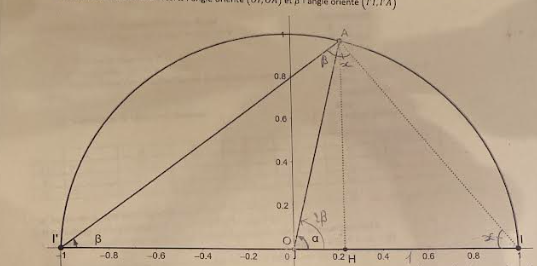
On considère un demi-cercle trigonométrique II'et un point A libre dessus. On appelle H le pied de la hauteur de 0AI issue de A. On note aussi a l'angle orienté (OI,0A) et ß l'angle orienté (I'I,l'A)Partie A :
- En vous aidant du résultat du devoir maison n°6, donner une relation entre a et B.
- Justifier que le triangle AII' est rectangle.
- Démontrer que I'H = 2 cos²(B).
Partie B : Cas 1 : 0 <= a <=π÷2
1) Exprimer 0H en fonction de a.
2) En déduire une relation reliant cos² (B) et cos(2ß).Partie C : Cas 2: π÷2<= a <=π
- Construire une nouvelle figure.
- Exprimer OH en fonction de a.
- En déduire une relation reliant cos² (B) et cos (2B).
Partie D :
- Quelle formule du cours aurait permis de démontrer cette relation ?
- Démontrer-la.
Merci d'avance pour votre aide.
-
@Noah-s Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
-
NNoah.s dernière édition par
cest la question 3 partie 1 qui me bloque
-
Exprime cos(β)cos(\beta)cos(β) dans les triangles I′AHI'AHI′AH et I′AII'AII′AI.
-
NNoah.s dernière édition par
c'est bon Jai réussi mais je suis bloqué a la question 2 partie c
-
Hhh02 dernière édition par
@Noemi
It looks like you might be trying to ask about finding the value of the cosine function in a right triangle using the letters 'B', 'AH', and 'AI'. In order to find the value of cos(B) in a right triangle, you will need to know the lengths of the sides of the triangle.The cosine of an angle in a right triangle is equal to the ratio of the length of the adjacent side to the length of the hypotenuse. If you know the lengths of the sides 'AH' and 'AI' and the angle 'B', you can use the following formula to find the value of cos(B):
cos(B) = AH / AI
If you don't know the lengths of the sides 'AH' and 'AI', or the angle 'B', you will not be able to find the value of cos(B).
-
La question 2 partie C, c'est la relation du cosinus dans le triangle rectangle AOHAOHAOH.
-
NNoah.s dernière édition par
@Noemi Merci pour cette information