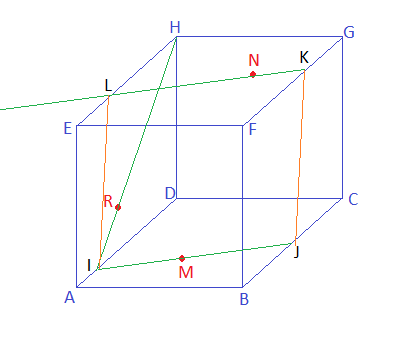
Intersection cube plan

Bonjour,
Déterminer l'intersection de du cube avec le plan (NRM).
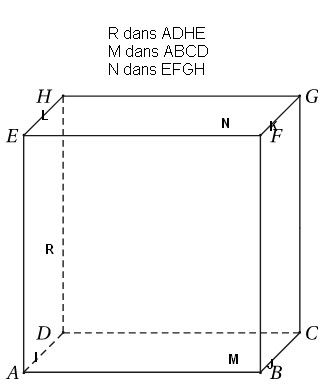
Cube inter plan.jpg
Comme mon imprimante est en panne, j'ai capturé un cube sur internet et j'ai mis les lettres en place avec photofiltre.
Le plan (HRM) coupe (AD) en I et ABCD en (IM).
(IM) coupe (BC) en J.
On trace la parallèle à (IJ) passant par N. Elle coupe (HE) en L et (FG) en K.
Donc LIJK est l'intersection de (NRM) avec le cube.
Je ne suis pas bien à l'aise avec les intersections plan-cube, plan-tétraèdre.
Est ce correct ?
Merci d'avance.

@kadforu , bonjour,

Ce n'est pas possible de te répondre clairement, car ton schéma n'est pas suffisant.
On sait dans quelles faces sont les points R,M,N mais on ne sait pas où ils sont positionnés dans les faces, ce qui est indispensable pour la construction.

Début de schéma

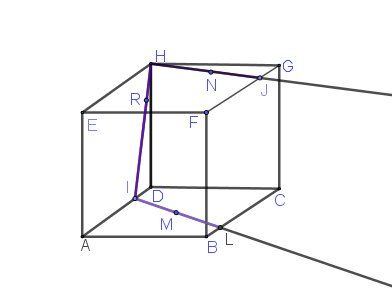
J'ai supprimé la section car elle était "boiteuse".

@mtschoon a dit dans Intersection cube plan :

@kadforu , bonjour,

Ce n'est pas possible de te répondre clairement, car ton schéma n'est pas suffisant.
On sait dans quelles faces sont les points R,M,N mais on ne sait pas où ils sont positionnés dans les faces, ce qui est indispensable pour la construction.

Pour l'exemple, je te mets une illustration, (sans savoir si la position des points convient...)

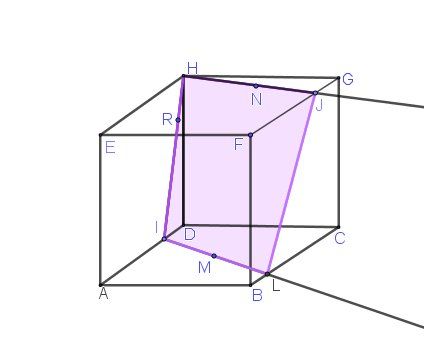
A justifier , bien sûr.
$(H R)$ coupe (AD) en $I$
$(H N)$ coupe (FG) en $J$
$(I M)$ coupe $(B C)$ en $L$
La section cherchée est $(H I L J)$

Bonjour,

Juste pour être sûr ...

Si la figure en mauve est bien un plan, pourquoi les droites d'intersection de ce plan avec 2 faces parallèles du cube ne sont-elles pas parallèles ?

Comme, par exemple sur ce dessin (piqué sur le net) qui n'est pas celui de l'énoncé ... mais où on voit bien le parallélisme invoqué dans ma remarque.

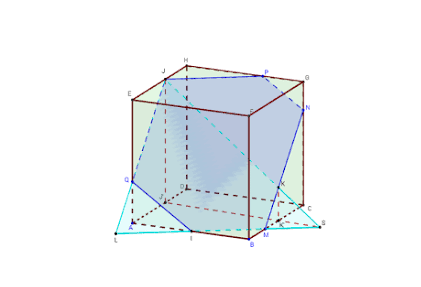
Sans titre.png

@Black-Jack , bonjour,

Ce ne sont pas les mêmes données dans le schéma que tu indiques.

Comme déjà signalé, ne sachant pas où sont véritablement positionnés les points R,M,N, on ne peut rien dire de l'explication de @kadforu .

Un autre exemple éventuel (plus proche des données car la section est déterminée par trois points situés sur les faces) .
Ce ne sont pas les mêmes faces, mais c'est la même idée :
http://www.debart.fr/geogebra_3D/geogebra_3D_premierre.html#ch24

Remarque :

@kadforu n'ayant pas pu faire un scan du schéma de l'énoncé, il aurait pu faire, avec un logiciel de construction gratuit( Geogébra, ou CabriGeomètre par exemple), une image représentative, pour plus de clarté.

Suivant les données, les sections peuvent être très différentes
Si je regarde les schémas que j'ai donnés dans des topics, il y en a de toute espèce...
C'est bien sûr très différent quand les points donnés sont sur les arêtes et non dans les faces.
Par exemple,
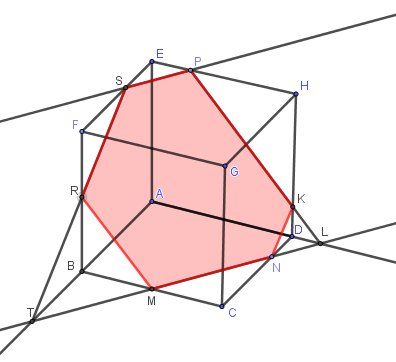
Cubemodifié.jpg

@mtschoon a dit dans Intersection cube plan :

@Black-Jack , bonjour,

Ce ne sont pas les mêmes données dans le schéma que tu indiques.

Comme déjà signalé, ne sachant pas où sont véritablement positionnés les points R,M,N, on ne peut rien dire de l'explication de @kadforu .

Un autre exemple éventuel (plus proche des données car la section est déterminée par trois points situés sur les faces) .
Ce ne sont pas les mêmes faces, mais c'est la même idée :&

http://www.debart.fr/geogebra_3D/geogebra_3D_premierre.html#ch24

Rebonjour,

Cela ne modifie pas mon interrogation,

Sur le dessin où on a juste une coin du cube coupé, on ne peut pas voir l'objet de ma remarque.
Néanmoins si on cherchait l'intersection du plan du triangle bleu avec le plan ABC(D), elle serait parallèle à la droite (PQ).
Ici on ne le voit pas car cette intersection est en dehors du cube ... mais cela ne change rien.

Quelles que soient les positions des points M,N, R (dans les plans mentionnés par l'énoncé), on devrait trouver que les intersections du plan MNR avec des plans des faces opposées du cube sont parallèles (même si elles sont pour certaines à l'extérieur du cube)

Sauf si je me trompe...

Dit autrement : Lorsqu'on trace la droite HR, I est dans le plan de la face ADHE du cube, et R est à la fois dans le plan ADHE et RMN ... mais pourquoi le plan RMN contiendrait-il le point H (et le I) ?

Si au lieu de commencer par tracer la droite HR et trouver le point I, on avait commencé par tracer la droite (ER), on aurait trouvé un point I sur (HD) ... et en continuant la construction le plan final en mauve aurait été différent ... Or l'intersection du plan RMN et du cube est unique, donc, sauf si je me trompe fortement, la construction faite n'est pas correcte.

@Black-Jack , je te suggère de donner ton schéma.
Le mien est "boiteux".
ça fait d'ailleurs 3 jours que la question a été posée...

Vu le manque d'indications données par @kadforu, je n'en fais pas davantage.

Rebonjour,

C'est sûr qu'un point dessiné sur une arête est parfaitement défini ...

Mais un point dessiné sur une face (précisée) l'est tout autant.

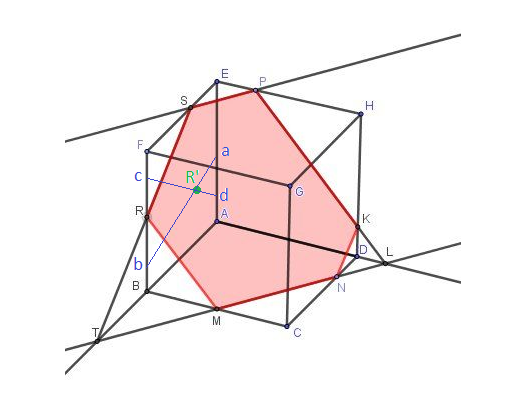
Par exemple, le point vert R' est dans le plan ABFE.

On trace 2 droites quelconques passant par R' ...
L'une coupe (AE) en a et (FB) en b
L'autre coupe (AE) en d et (FB) en c

Les points a, b, c et d sont sur des arêtes du cubes et donc parfaitement situés.
Et comme R' est à l'intersection de 2 droites ((ab) et (ac)) parfaitement situées par leurs intersections avec les arêtes du cube ... R' est parfaitement déterminé.

Par là, il devrait être possible de construire l'intersection du plan RMN de l'énoncé avec le cube ... mais c'est plus compliqué avec des points R, M et N sur des faces du cube et pas sur les arêtes.

Et cette intersection sera avec des droites // sur les plans des faces opposées du cube.

Sauf si je me trompe.

Sans titre.png

J'ai tiqué sur le résultat donné qui ,pour moi, n'est pas correct et j'ai pensé que je devais le mentionner ...

Pour ma construction ... je n'ai pas essayé et je ne sais pas si j'y arriverai ...

Bonjour et bonne année à tout le monde.

Théorème ou propriété (je ne sais pas trop):
Deux plans parallèles coupés par un plan, les droites d'intersection sont parallèles.

@kadforu , bonjour et bonne année à toi aussi.

Tout à fait d'accord @kadforu , c'est pour ça que j'ai traité mon schéma de "boiteux".
Si tu as une véritable construction à proposer, ce serait bien .

Comme déjà indiqué, tu pourrais t'inspirer de celui-ci qui est du même type ( 3 points sur des faces).
http://www.debart.fr/geogebra_3D/geogebra_3D_premierre.html#ch24

Bon, J'ai réussi à tracer l'intersection en utilisant les outils de photofiltre.
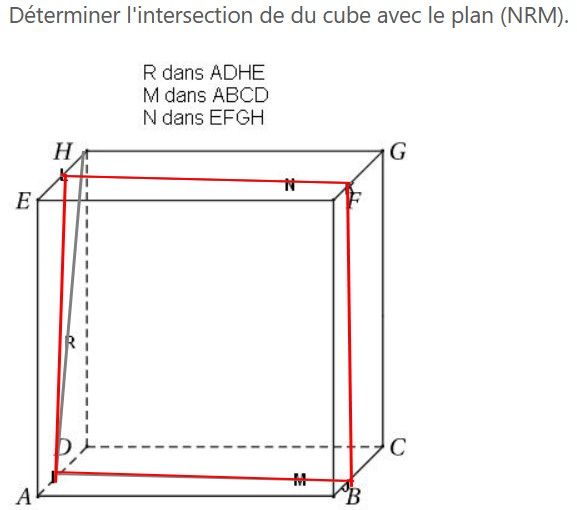
Cube inter plan.jpg

les points R, M et N sont là ou' il figurent sur le dessin comme si c'était des croix ( un point est noté par une croix).
Le plan (HRM) coupe (AD) en I et ABCD en (IM).
(IM) coupe (BC) en J.
J'utilise la propriété des plans parallèles:
Je trace la parallèle à (IJ) passant par N. Elle coupe (HE) en L et (FG) en K.
Donc LIJK est l'intersection de (NRM) avec le cube.

Rebonjour,

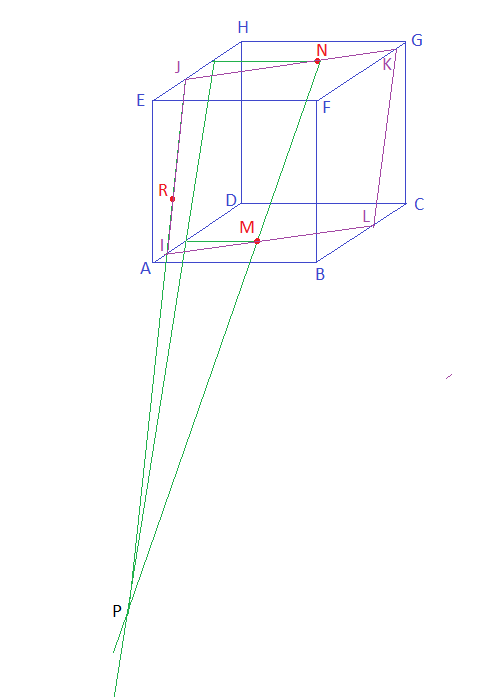
Proposition :

On cherche le point de percée P de la droite (MN) dans le plan AEHD

On trace la droite (PR) qui coupe (AD) et (EH) aux points I et J qui sont sur l'intersection de la bace AEHD du cube et le plan MNR.

On complète le tracé de l'intersection en traçant (JN) qui coupe (GF) en K et en traçant (AM) qui coupe (BC) en L.

IJKL est l'intersection cherchée.

Il se peut que, suivant les positions imposées des points R, M et N, que certains des points I, J, K et L soient en dehors des arêtes du cube ... cela complique un peu, mais pas beaucoup.

Toutes sottises incluses.

Sans titre.png

Bonjour,
1°)

On trace la droite (PR)

Comment tu traces cette droite si avant tu ne connais pas le point P ?

en traçant (AM) qui coupe (BC) en L.

Plutôt la droite (IM).
2°)
J'ai compris ta méthode mais pas le point P
Mais est ce que ma méthode est juste ? Autrement dit, si ma démarche est juste ?

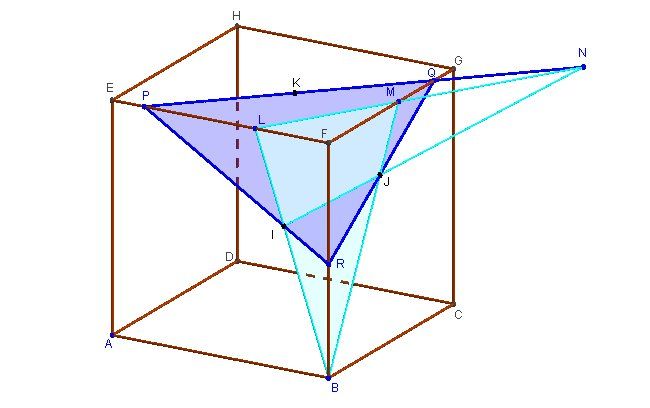
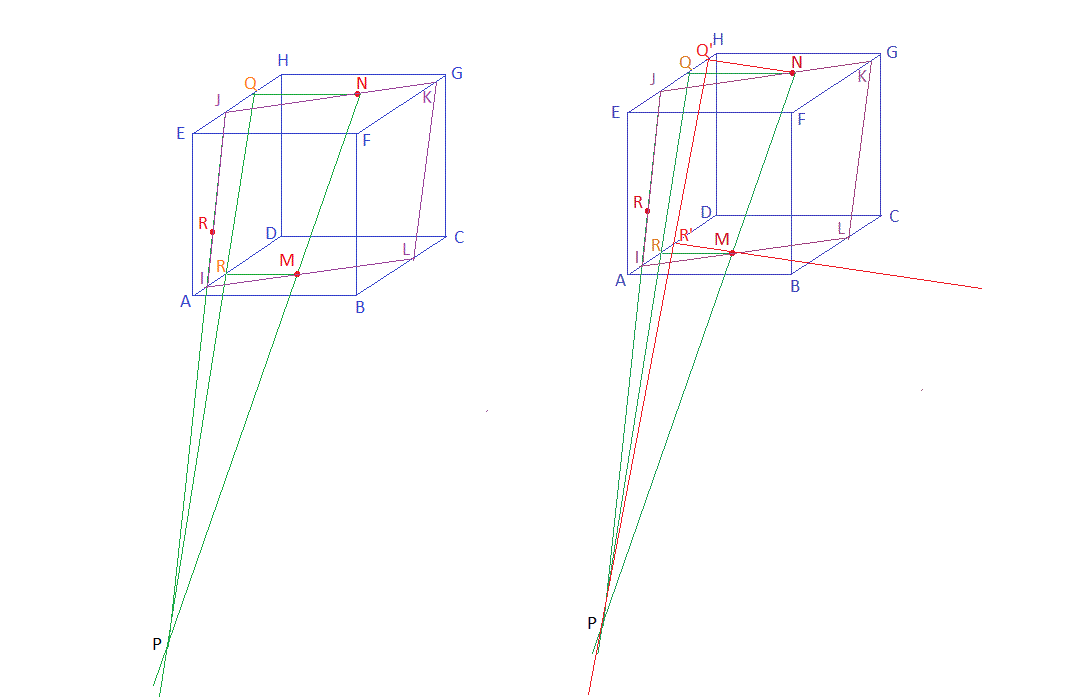
Sur le dessin de gauche :

Par N on trace la droite (NQ) avec Q sur (HE)
par M on trace la droite (MR) parallèle à (NQ), elle coupe (AD) en R.

P est à l'intersection des droites (MN) et (QR)

Remarque, on pouvait tracer la droite (NQ) dans une direction quelconque et suivre la même construction que ci-dessus.
Par exemple, sur le dessin de droite, j'ai tracé une autre droite (NQ')
... qui a permis de trouver le point R'
et (Q'R') passe aussi par P

P est le point de percée de la droite (MN) dans le plan (ADHE)

Sans titre.png

Excuse moi si je deviens un peu lourd mais comment est obtenu le point Q ?

Oui, je n'ai pas fait attention à la construction du point Q.

@kadforu a dit dans Intersection cube plan :

Excuse moi si je deviens un peu lourd mais comment est obtenu le point Q ?

Quelques bisbrouilles sur les lettres dans mes dessins où j'ai noté 2 point différents par la même lettre, j'essaie de remettre sur pieds (sauf nouvelle étourderie)

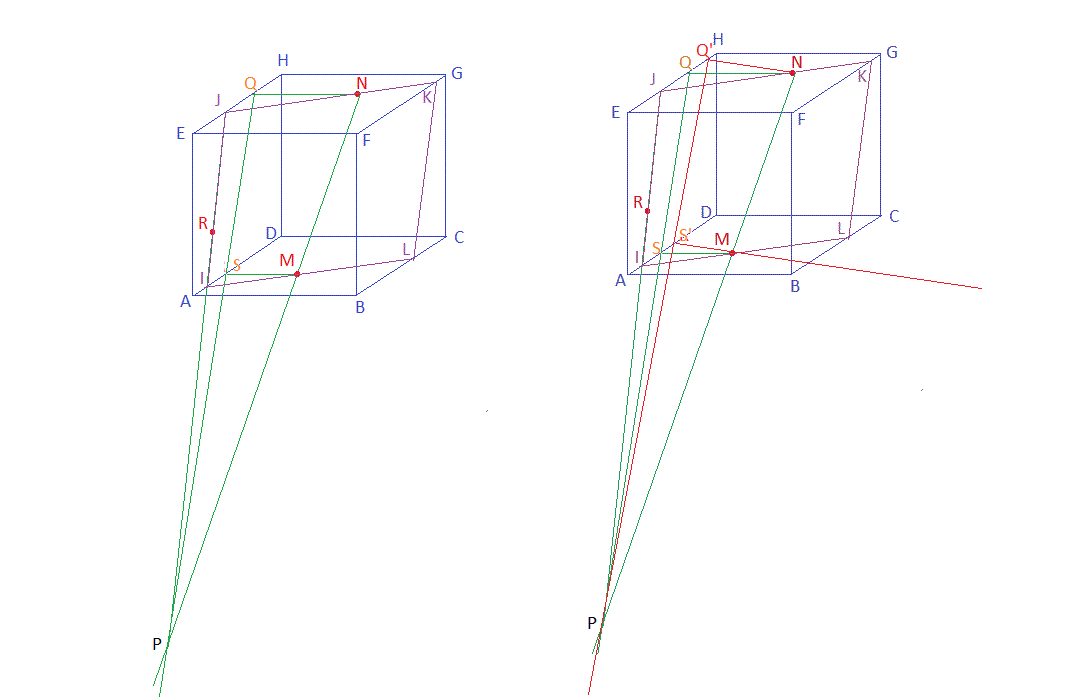
Regarde ceci avec les dessins et le texte corrigé ... repose une question si tu ne comprends pas.

Sur le dessin de gauche :

Par N on trace la droite (NQ) avec Q sur (HE)
par M on trace la droite parallèle à (NQ), elle coupe (AD) en S.

P est à l'intersection des droites (MM) et (QS)

Remarque, on pouvait tracer la droite (NQ) dans une direction quelconque et suivre la même construction que ci-dessus.
Par exemple, sur le dessin de droite, j'ai tracé une autre droite (NQ')
... qui a permis de trouver le point S'
et (Q'S') passe aussi par P

P est le point de percée de la droite (MN) dans le plan (ADHE)

Sans titre.png

J'ai vu sur internet qu'on commence par un sommet du cube, c'est pour ça j'ai commencé par tracer le plan HIM.

@kadforu a dit dans Intersection cube plan :

J'ai vu sur internet qu'on commence par un sommet du cube, c'est pour ça j'ai commencé par tracer le plan HIM.

Pourquoi ton point I serait-il dans le plan NRM ?
Sa position, comme tu as procédé, ne dépend pas du point N et cela ne peut pas être correct.

Pourquoi ton point I serait-il dans le plan NRM ?

Le plan (HRM) coupe (AD) en I et ABCD en M
(IM) dans (HRM) et (RM) dans (HRM)
Comme (IM) et (RM) ne sont pas parallèles alors elles se coupent en M.
Donc I dans (NRM).

@kadforu a dit dans Intersection cube plan :

Pourquoi ton point I serait-il dans le plan NRM ?
Le plan (HRM) coupe (AD) en I et ABCD en M
(IM) dans (HRM) et (RM) dans (HRM)
Comme (IM) et (RM) ne sont pas parallèles alors elles se coupent en M.
Donc I dans (NRM).

Ce ne peut pas être juste.
Dans les 3 premières lignes de ton explication, il n'est nulle part fait mention du point N.

Et puis subitement tu conclus que "Donc I dans (NRM)" conclusion qui devrait dépendre de la position du point N qui n'a pas été évoqué dans le reste du raisonnement.

C'est faux.

Dans les 3 premières lignes de ton explication, il n'est nulle part fait mention du point N.

Je l'ai expliqué dans mon premier message:
Les faces ABCD et EFGH sont parallèles.
(IJ) dans ABCD.
D'après la propriété des plans parallèles, je trace la parallèle à (IJ) passant par N. Elle coupe (HE) en L et (FG) en K.

Mais je ne prétends pas que j'ai raison, je ne suis qu'un élève et c'est pour ça je demande de l'aide.

Les faces ABCD et EFGH sont parallèles.
(IJ) dans ABCD.
D'après la propriété des plans parallèles, je trace la parallèle à (IJ) passant par N. Elle coupe (HE) en L et (FG) en K.

Mais je ne prétends pas que j'ai raison, je ne suis qu'un élève et c'est pour ça je demande de l'aide.

/////////////////////////////////

Je ne sais pas comment te faire admettre l'évidence, j'ai donné les explications qui montrent que ta construction n'est pas bonne.

Je réessaie en faisant un dessin plus clair que le tien où tout est massacré.

Peu importe que les points M, N et R soient où non pile aux même endroits que sur ton énoncé. Si le principe de ta construction était bonne, elle marcherait aussi pour ce nouveau dessin.

J'applique ta construction :

On trace (HR) qui coupe (AD) en I
On trace (IM) qui coupe (BC) en J
Le plan (HIJ) comprend bien les points R et M

On trace la parallèle à (IJ) passant par N
Et cette parallèle coupe (FG) en K et (EH) en L

Et tu prétends que LIJK est l'intersection de (NRM) avec le cube.

Mais c'est faux car R n'appartient pas au plan IJKL.
Cela se voit clairement sur ce dessin car R n'appartient pas à (IL)

OK ?
Sans titre.png