ETUDES FONCTION [ Besoin d'aide ]
-
Robz dernière édition par
Bonjour, j'aurais besoin d'aide pour étudier cette fonction, en vous remerciant d'avance.
f(x) = x*exp(2x/x²-1)
- Déterminer le domaine de définition Df de la fonction f
- Déterminer les limites de f aux bornes de Df
- Etudier les asymptotes à sa courbe Cf . On prouvera notamment l'existence d'une branche infinie (d).
- Montrer que f est dérivable et calculer sa dérivée
J'ai commencé ce que je sais faire ( enfin je pense ) :
- Je pense que le domaine de définition c'est R+* étant donné que x#-1, x#1.
- Dérivée : f'(x) = -4 * exp * x/(x²-1)²
-
@Robz Bonsoir,
Le domaine de définition Df=R−{−1;1}D_f= R-\lbrace -1;1\rbrace Df=R−{−1;1}
Vérifie la dérivée.
Si f(x)=xe2xx2−1f(x)= xe^{\frac{2x}{x^2-1}}f(x)=xex2−12x
f′(x)=e2xx2−1+x×2(x2−1)−2x×2x(x2−1)2e2xx2−1=....f'(x) = e^{\frac{2x}{x^2-1}}+x\times \dfrac{2(x^2-1)-2x\times2x}{(x^2-1)^2}e^{\frac{2x}{x^2-1}} = ....f′(x)=ex2−12x+x×(x2−1)22(x2−1)−2x×2xex2−12x=....
je te laisse vérifier et poursuivre.
-
mtschoon dernière édition par mtschoon

Bonsoir,
@Robz ,
Si tu veux consulter tes réponses pour les limites aux bornes de l'ensemble de défintion ( x tend vers +∞+\infty+∞,−∞-\infty−∞, −1-1−1 (à gauche et à droite) , +1+1+1 (à gauche et à droite), regarde le schéma.Tu as même l'asymptote oblique (d'équation y=x+2)
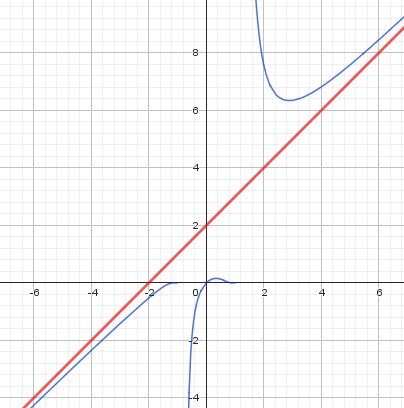
Reposte si besoin.