SOS Enigme Dénombrement

Bonjour,

Voici plusieurs jours que je tourne en rond face à cette énigme ... quelqu'un pour m'aider ?

Au restaurant, un groupe de 8 personnes choisit sur une carte contenant 8 entrées. Chaque entrée de la carte a été choisi par exactement 5 personnes.
Montrer que, dans toutes les situations possibles, il y aura au moins deux personnes qui, à eux deux, auront goûté toutes les entrées de la carte

Merci d'avance

@Alec100dre Bonjour,

L'énoncé est-il complet ?

@Noemi Bonjour,
J'espère car c'est celui que l'on m'a distribué

@Alec100dre

Il n'est pas indiqué le nombre d'entrée choisi par une personne ?

et non ... c'est certainement ce qui fait le sel de cette énigme

@Alec100dre
C'est un problème de compréhension de l'énoncé notamment de la phrase chaque entrée de la carte a été choisi par exactement 5 personnes.

Pour l'instant je suis à l'étape schéma :
8 personnes P1 ; P2 ; P3 ; P4 ; P5 . P6 ; P7 et P8
8 entrées sur la carte : e1 ; e2 ; e3 ;e4 ; e5 ; e6; e7 et e8

Chaque entrée (ei) a été choisie par exactement 5 personnes : exemple e2 a été choisie par {P2 ; P4 ; P6 ; P7 ; P8}

@Alec100dre

Ecris une répartition possible pour chacune des entrées.

sauf erreur de ma part il y a 56 combinaisons par entrée ... je ne vois pas comment toutes les écrire ?

@Alec100dre

Juste écrire 8 combinaisons possibles correspondant aux 8 entrées.
$e_1 : ( P_1 ; P_2 ; P_3 ; P_4; P_5)$
$e_2 : ( P_2 ; P_3 ; P_4; P_5 ; P_6)$
....

le problème est que :
e1 : (P1 P2 P3 P4 P5) n'empêche pas que e2 : (P1 P2 P3 P4 P5) aussi ...

@Alec100dre

Oui,
mais je fais juste une proposition pour que 5 personnes aient choisies chaque entrée, en partant de chaque entrée et en modifiant une personne.

$e_1 : ( P_1 ; P_2 ; P_3 ; P_4; P_5)$
$e_2 : ( P_2 ; P_3 ; P_4; P_5 ; P_6)$
$e_3 : ( P_3 ; P_4 ; P_5 ; P_6; P_7)$
$e_4 : ( P_4 ; P_5 ; P_6; P_7 ; P_8)$
$e_5 : ( P_5 ; P_6 ; P_7 ; P_8; P_1)$
$e_6 : ( P_6 ; P_7 ; P_8; P_1 ; P_2)$
$e_7 : ( P_7 ; P_8 ; P_1 ; P_2; P_3)$
$e_8 : ( P_8 ; P_1 ; P_2; P_3 ; P_4)$

et donc, pour cet exemple, P5 et P2 ont bien à eux deux gouté toutes les entrées.

Mais je ne vois pas comment généraliser ...

@Alec100dre

Tu aurais pu choisir $P_4$ et $P_7$
Avec 8 situations, on montre qu'il y a au moins une possibilité, donc si on écrit toutes les situations possibles, ....

Bonjour/bonsoir,

Le regarde cet énoncé.

Une idée peut-être pour l’éclaircir.

La première phrase de l’énoncé est volontairement très très floue…
Il faut regarder la question posée pour s’apercevoir que l’on peut considérer (je pense ! ) que chaque personne a pu « goûter/choisir » entre une et huit entrées...
La seconde phrase est claire car chaque entrée est choisie par exactement 5 personnes

Je suggère une disposition pratique pour clarifier et pouvoir raisonner avec.

Par exemple, dans un repère du plan, en abscisse, mettre les numéros des entrées (de 1 à 8 ) et en ordonnée les numéros des personnes (de 1 à 8 ).
On peut ainsi obtenir un quadrillages dont des points d’intersection auront en abscisse le numéro de l’entrée et en ordonnée le numéro de la personne.
C’est que que j’ai fait dans le schéma joint.

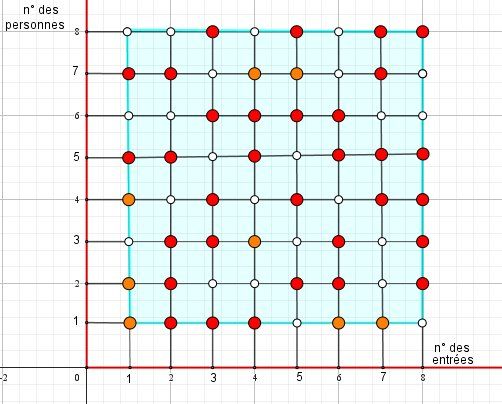
Remarque : on peut faire aussi un damier (8x8), ce qui reviendrait au même, mais qui serait certainement plus « ludique » !

Les grosses boules rouges représentent les points « solutions »
Par colonne il y en a donc 5. Au total, il y en a 5 x 8=40

Les petites boules blanches sont les intersections non occupées ; il y en donc 64-40=24.

Avec ça, on peut tenter de raisonner sur toutes les dispositions possibles, en fonction des lignes.

Les 24 boules blanches peuvent être disposées sur 3 ou 4 ou 5 ou 6 ou 7 ou 8 lignes.

1er cas : les 24 boules blanches sont disposées sur 3 ou 4 ou 5 ou 6 ou 7 lignes
Ainsi au moins une ligne contiendra en totalité des boules rouges donc réponse prouvée.

2ème cas : les 24 boules blanches sont disposées sur 8 lignes ( c’est à dire au moins une boule blanche par ligne)
C’est le cas du schéma joint.
Je n’ai pas « creusé » mais je me demande si un raisonnement par l’absurde ne conviendrait pas.

Bonne réflexion et bon courage !

pas mal la présentation sous forme de quadrillage : une matrice !

J'ai aussi pensé à l'absurde ( présence du au moins ) : quelque soit i et j il existe k tel que ek n est choisie ni par Pi ni par Pj ...

@Alec100dre ,

Oui , tout à fait une matrice.
C'est du moins comme ça que je conçoit l'énoncé.
Tu peux mettre par exemple, $1$ pour boule rouge et $0$ pour boule blanche.