Géométrie Trapèze à partager

Bonsoir
J'ai un dm pour mercredi 1er février et je me casse la tête dessus, pouvez vous m'aidez s'il vous plait ?
Voici l'énoncé:
Les deux classes gagnantes du rallye mathématiques auront à se partager en parts égales un gâteau. Celui-ci
a la forme d’un trapèze ABCD dont les côtés parallèles ont pour longueurs AB = 54 cm et CD = 26 cm.
A quelle distance de A doit-on placer un point E entre A et B de façon que le segment [DE] partage le
gâteau en deux parties de même aire ?
Merci pour votre aide
Melvil

Bonjour,
Il y a une "indélicatesse" dans l'énoncé.

Si on respecte les usages, il aurait fallu nommer le trapèze ABDC et pas ABCD.

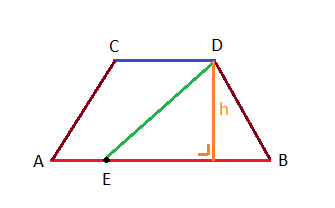
Sans titre.png

Poser AE = x

Aire du trapéze ABDC $\frac{AB + CD}{2} * h$ (avec AB et CD connus)

Aire du triangle EBD $\frac{EB * h}{2}$ avec EB = AB - x

Et puis écrire la relation 2 * (Aire du triangle EBD) = Aire du trapéze ABDC

...

@Black-Jack
Merci beaucoup pour votre aide Black-jack.
J'avais pris la même méthodologie mais l'indélicatesse m'a perturbé. Il fallait votre assurance.
Je vais l'appliquer et je vous reviens en cas de soucis.

Ce message a été supprimé !

@Black-Jack a dit dans Géométrie Trapèze à partager :

@Melvil a dit dans Géométrie Trapèze à partager :

@Black-Jack
Merci beaucoup pour votre aide Black-jack.
J'avais pris la même méthodologie mais l'indélicatesse m'a perturbé. Il fallait votre assurance.
Je vais l'appliquer et je vous reviens en cas de soucis.

Bonjour,

Désolé ... mais j'ai été distrait.
L'énoncé tel qu'il est donné est également correct.

Avec ce dessin :

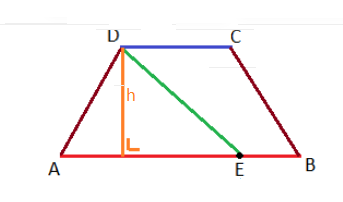
Lé résolution est presque la même.

Sauf qu'ici c'est l'aire du triangle ADE qu'on doit considérer :

Aire du triangle ADE = $AE∗h2\frac{AE * h}{2}$ avec AE = x

Et puis écrire la relation 2 * (Aire du triangle ADE) = Aire du trapéze ABCD

Sauf nouvelle distraction.

@Black-Jack
Merci
Du coup une fois dessiné, on connait h pour trouver x ?

Bonjour,

@Melvil , en se basant sur le graphique correspondant à l'énoncé :

Comme te l'a indiqué Black-Jack,

$aire(ABCD)=(54+262)×h=40haire(ABCD)=\biggr(\dfrac{54+26}{2}\biggr)\times h=40h$

$2 a i r e (A D E) = a i r e (A B C D) = 40 h$

donc : $a i r e (A D E) = 20 h$

or, $(ADE)=\dfrac{h\times x}{2}$

Tu as donc l'égalité : $h×x2=20h\dfrac{h\times x}{2}=20h$

$h$ n'est pas nul.
Tu peux simplifier par $h$ et tu obtiendras $x$ .

Tu peux donner ta réponse si tu souhaites une vérification.

@mtschoon
Merci beaucoup de votre précieuse aide

De rien @Melvil .
Nous faisons au mieux.
J'espère que tu as trouvé $x = 40$ (cm)