Bonjour tout le monde

voila l'énoncé :
On considère la fonction définie sur ]0,+l'infini[ par f(x) = (√ₓ²+1) ⁄ₓ
A/ 1) Etudier la dérivabilité de f sur ]0,+l'infini[
2)a) Montrer que : f'(x)=₋1 ⁄ ₓ²√ₓ₂+1
b) En déduire que : f(x)>1 pour tout x>0
Je n'arrive pas à comprendre la relation entre f(x) et la question qui précède.
Merci pour votre aide en avance.

@Lou-Puppet bonsoir,
Mettre la formule de politesse dans le texte, mais pas dans le titre.
Le titre doit correspondre à la question posée.

Si j'ai bien lu , pour $x>0x\gt 0$
$f(x)=x2+1xf(x)=\dfrac{\sqrt{x^2+1}}{x}$
$f′(x)=−1x2x2+1f'(x)=\dfrac{-1}{x^2\sqrt{x^2+1}}$

Piste à expliciter ,

$f′(x)<0f'(x)\lt 0$ donc f strictement décroissante sur $]0,+∞[]0,+\infty[$

Tu peux faire le tableau de variation de $f$ sur $]0,+∞[]0,+\infty[$

$lim⁡x→+∞f(x)=1\displaystyle \lim_{x\to +\infty}f(x)=1$ (à prouver)

(La limite en 0 n'est pas indispensable)

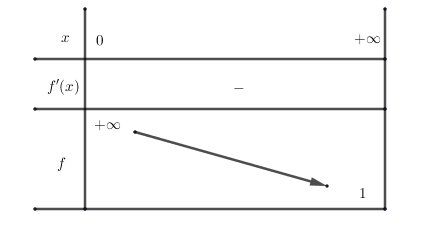
Conséquence $f(x)>1f(x)\gt 1$ pour tout $\gt 0$

@mtschoon Merci pour votre réponse.

De rien @Lou-Puppet .
J'espère que tout est clair pour toi.