SVP j ai besoin d aide dans un exercice de polynôme
-
Anwar Ben Brahim dernière édition par
Bonjour
Comment je montre que un polynôme de degré 2n+1 doit nécessairement avoir une racine réelle
-
mtschoon dernière édition par mtschoon

@Anwar-Ben-Brahim , bonjour,
Cette question n'est pas facile à expliquer au niveau Première...
Je te donne une idée, mais adapte en fonction de ton cours.Tu n'indiques rien sur nnn ...
Je suppose que n est un naturel.Piste,
Soit P(x)=a2n+1x2n+1+a2n+...+a0P(x)=a_{2n+1}x^{2n+1}+a_{2n}+...+a_0P(x)=a2n+1x2n+1+a2n+...+a0 avec a2n+1≠0a_{2n+1}\ne 0a2n+1=0P est une fonction polynôme, définie dérivable donc continue sur RRR
En −∞-\infty−∞ et +∞+\infty+∞, la limite d'un polynôme est la limite de son terme de plus fort degré , donc ici de a2n+1x2n+1a_{2n+1}x^{2n+1}a2n+1x2n+1
1er cas : Soit a2n+1>0\boxed{a_{2n+1}\gt 0}a2n+1>0
limx→−∞P(x)=−∞\displaystyle \lim_{x\to -\infty}P(x)=-\inftyx→−∞limP(x)=−∞
limx→+∞P(x)=+∞\displaystyle \lim_{x\to +\infty}P(x)=+\inftyx→+∞limP(x)=+∞
Vu la continuité de PPP, PPP est une application de RRR vers RRR
Tout élément de RRR (ensemble d'arrivée) a au moins un antécédent dans l'ensemble RRR de départ.
En particulier 000 (de l'ensemble d'arrivée) a au moins un antécédent x0x_0x0 dans l'ensemble R de départ.L'équation P(x)=0P(x)=0P(x)=0 a donc au moins une solution réelle x0x_0x0
Illustration graphique
x0x_0x0 est l'abscisse de AAA
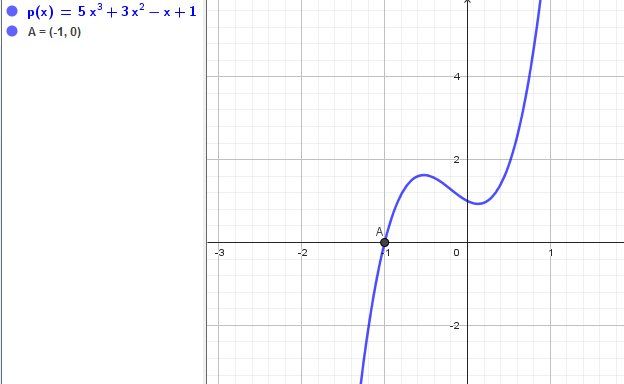
-
mtschoon dernière édition par mtschoon

2ème cas : Soit a2n+1<0\boxed{a_{2n+1}\lt 0}a2n+1<0
limx→−∞P(x)=+∞\displaystyle \lim_{x\to -\infty}P(x)=+\inftyx→−∞limP(x)=+∞
limx→+∞P(x)=−∞\displaystyle \lim_{x\to +\infty}P(x)=-\inftyx→+∞limP(x)=−∞Vu la continuité de PPP, PPP est une application de RRR vers RRR
Tout élément de RRR (ensemble d'arrivée) a au moins un antécédent dans l'ensemble RRR de départ.
En particulier 000 (de l'ensemble d'arrivée) a au moins un antécédent x0x_0x0 dans l'ensemble R de départ.L'équation P(x)=0P(x)=0P(x)=0 a donc au moins une solution réelle x0x_0x0
Illustration graphique
x0x_0x0 est, par exemple, l'abscisse de AAA
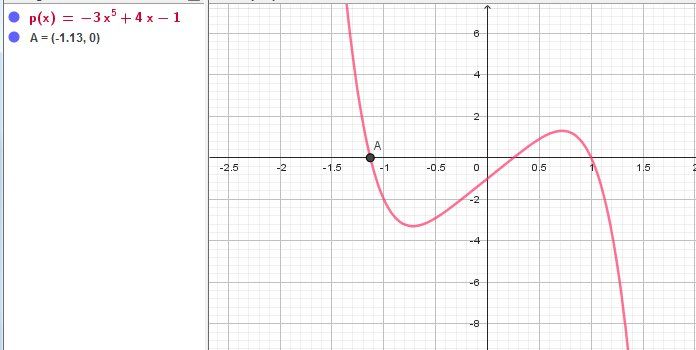
Reposte si besoin.
-
Anwar Ben Brahim dernière édition par
Merci beaucoup
-
mtschoon dernière édition par

De rien @Anwar-Ben-Brahim et bon travail .