Etude de fonctions périodiques
-
Mmanooonnnnn dernière édition par
Bonjour,
Pourriez-vous me décrire les différentes étapes à suivre, pour montrer qu'une fonction est périodique/ apériodique dans le cas de ces deux fonctions?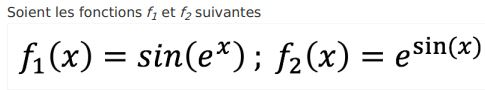
Merci d'avance!
-
@manooonnnnn Bonjour,
Attention, le multipost est interdit sur ce forum. L'autre post va être supprimé.
Utilise la définition de fonction périodique.
-
mtschoon dernière édition par mtschoon

Bonjour,
@manooonnnnn , comme te l'indique Noemi, commence par consulter la définition de ton cours.
Si besoin, regarde ici :
http://serge.mehl.free.fr/exos/periode.htmlSi tu as une doute sur une fonction , je te conseille de commencer par la représenter graphiquement sur ta calculette et d'observer.
Pour la fonction f1f_1f1
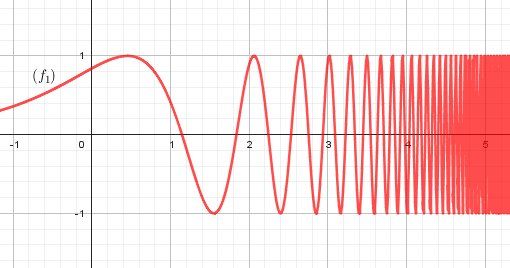
A l'évidence, elle n'est pas périodique !Bien que ce ne soit pas le but (car on cherche la périodicité pour restreindre l'étude d'une fonction) , tu dois pouvoir démontrer qu'elle n'est pas périodique en faisant un raisonnement par l'absurde.
-
mtschoon dernière édition par mtschoon

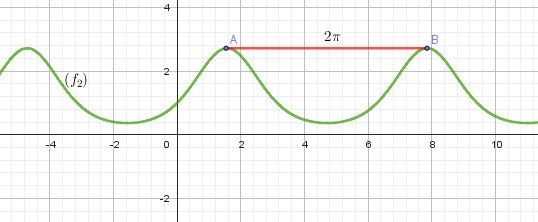
Pour la fonction f2f_2f2
Il n'y a pas de doute.
Tu sais que la fonction sinus est 2π2\pi2π- périodique (2π2\pi2π est la période "fondamentale") et que la fonction exponentielle ne l'est pas, donc f2f_2f2 est périodique et la période de f2f_2f2 est la période de la fonction sinus.Pour tout x réel :
sin(x+2π)=sin(x)sin(x+2\pi)=sin(x)sin(x+2π)=sin(x)
donc esin(x+2π)=esin(x)e^{sin(x+2\pi)}=e^{sin(x)}esin(x+2π)=esin(x)
donc f2(x+2π)=f2(x)f_2(x+2\pi)=f_2(x)f2(x+2π)=f2(x)
d'où la conclusion : f2f_2f2 est 2π2\pi2π- périodique
Remarque
Lorsque tu as une fonction composée de la forme gofgofgof avec fff de période TTT et ggg non périodique , gofgofgof est de période TTT
C'est le cas de f2f_2f2Bonne réflexion !