Exercice de dérivation

[Enzo Brzezinski]

Bonjour à toutes et à tous.
Je suis actuellement un élève de première S qui a décidé de prendre des cours de mathématique en plus pendant les vacances avant son passage en Tale
je dois rendre un devoir de mathématiques pour ce lundi cependant je me retrouve bloqué sur un des de mes 6 exercices , j'aimerai si possible une aide , un indice ou un raisonnement à avoir pour le réaliser car je n'avance plus
Voici l'intitulé
Dans un repère orthonormé (O,i,j) on a représenté ci-contre la fonction f défini sur l'intervalle [0;3] par f(x)=9-x^2 On note C sa représentation graphique .
A est un point mobile sur C , c et B sont des points respectivement sur l'axe des abscisses et l'axe des ordonnées tels que OCAB soit un rectangle
On veut déterminer où placer le point A pour que le rectangle OCAB ait une aire maximale.
Merci de votre et de votre attention même si vous ne répondez pas.
Bonne journée à tous.[texte du lien](url du lien)

[mtschoon]

@Enzo-Brzezinski , bonjour ,

Un graphique pour éclairer ton énoncé,

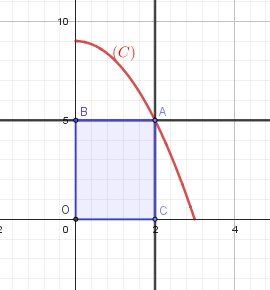
Piste pour démarrer,

Soit $x$, compris entre $0$ et $3$, l'abscisse de $A$

Les coordonnées de $A,B,C$ sont :
$A(x,9-x^2)$
$B(0,9-x^2)$
$C(x,0)$

Tu peux en déduire : $AB=x$ et $AC=9-x^2$

$aire(OCAB)=AB\times AC=x(9-x^2)$

Tu étudies les variations de $g$ définie par $g(x)=x(9-x^2)$, pour $x\in [0,3]$ et tu en déduis la valeur de $x$ pour laquelle $g(x)$, c'est à dire l'aire$(OCAB)$, est maximale.

Reposte si besoin.