fonction f donné par son tableau de variation

Bonjour quelqu'un pourrait t'il m'aider pour cette exercice ? En vous remerciant.

x : −∞ −2 1 +∞
Signe de f′(x): − + −

Variations de f: +∞ - {(e)}^{ -2 } 5{(e)}^{ -1 } 0

Dire si chacune des affirmations est vrai ou fausse et justifier.
1- L'image de -3 par f est plus petite que l'image de 2 par f.
2-f'(-3) > f’(-2)
3- Il existe un unique antécédent de 0 par f sur ]-∞ ; -2[
4-f(7) ≥ f(-2)
5- 0,5 est solution de l'équation f’(x) > 0
6- f est positive sur [- 1; +∞ [
7- Si F est une primitive de f, alors on sait que F est décroissante sur [I;+∞ [
8- F’(-2)<0
9- La représentation graphique de f admet une asymptote en +∞
10- La représentation graphique de F n'admet aucune tangente horizontale sur [-2,1].

jai pense avoir les bonne reponse mais je ne suis pas sure
1- faux
2-faux
3-vrai
4-vrai
5-vrai
6-faux
pour la suite je ne comprend pas
Merci pour votre aide

@Noah-s Bonjour,

L'énoncé est complet ?
Pas de représentation graphique ?

oui il n'y a pas de représentation graphique

Bonjour,

Vu le titre "fonction f donnée par son tableau de variation", je pense que le tableau de variation est donné et que @Noah-s a voulu l'indiquer, à sa façon, dans les premières lignes de son message.

J'ai tenté de le reconstituer :

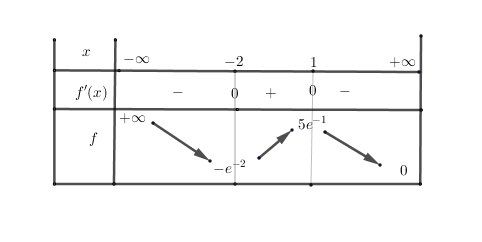
Merci à @Noah-s d'indiquer si ma reconstitution est exacte ou non.

oui cest exactement ca

@Noah-s

La réponse à la question 6 est à revoir.
pour la question 7, étudier le signe de la fonction $f$ .
Question 8, quel est le signe de $f (- 2)$ ?
Question 9, si $x$ tend vers $+∞+\infty$ , $f (x)$ tend vers ....
Question 10, quel est le signe de $f (x)$ sur l'intervalle indiqué ?

pour moi de [- 1; +∞ [ on ne peut pas savoir car f(-2) est negatif

pour la 7 comment je peut etudier le signe de la fonction sachant qu eje nai pas la fonction
pour la 8 je ne comprend pas a quoi sa sert d'avoir le signe de f(-2) je sais qu'il est négatif
pour la 9 je pense que cest vrai elle admet une asymptote en x tend vers +∞ f(x) tend vers 0
pour la 10 de signe de f(x) est positif mais je vcomprend pas a quoi ca nous sert

@Noah-s , rebonjour,

@Noah-s a dit dans fonction f donné par son tableau de variation :

pour moi de [- 1; +∞ [ on ne peut pas savoir car f(-2) est negatif

Je pense que tu parles de la question 6.

Effectivement, tu ne peux répondre ni par "vrai" ni par "faux"

Avec le TVI, tu peux justifier qu'il existe une valeur $α\alpha$ comprise entre $- 2$ et $1$ telle que $f(α)=0f(\alpha)=0$
Ansi, sur $[α,+∞[,f(x)≥0[\alpha, +\infty[, f(x)\ge 0$
Mais , tu ne peux pas savoir si $α\alpha$ est inférieur ou supérieur à $- 1$
L'énoncé aurait dû, par exemple, donner la proposition : "f est positive sur $[−2,+∞[[-2,+\infty[$ "

@Noah-s , je regarde un peu la suite.

Pour la 7), je te mets un lien qui traite "primitive , intégrale , aire" :
https://www.youtube.com/watch?v=CldGgW3sSN8

Sur $[1,+∞[[1,+\infty[$ , f prend des valeurs positives; lorsque x varie de $1$ à $+∞+\infty$ , l'aire "sous la courbe" augmente.
Tu tires la conclusion

Pour la 8), si c'est bien de F'(-2) dont il s'agit (comme indiqué) , $F^{'} = f$
donc la proposition peux s'écrire $f(−2)<0f(-2)\lt 0$
Tu tires la conclusion

Pour la 9), $lim⁡x→+∞f(x)=0\displaystyle \lim_{x\to +\infty}f(x)=0$ donc l'axe des abscisses est asymptote horizontale à la courbe
Tu tires la conclusion

Pour la 10),
Si c'est bien de de F dont il s'agit (comme indiqué) , tu cherches une valeur de $x$ telle que $F^{'} (x) = 0$ c'est à dire $f (x) = 0$
Il y a deux valeurs de $x$ qui satisfont à cette condition (une inférieure à $- 2$ et une autre entre $- 2$ et $1$ )
Tu tires la conclusion

Remarque : Si c'est de $f$ dont il s'agit, $f^{'} (- 2) = 0$ donc tangente horizontale à la courbe pour $x = - 2$
$f^{'} (1) = 0$ donc tangente horizontale à la courbe pour $x = 1$
Tu tires la conclusion

Bonnes réflexions.

daccord merci pour votre aide.

De rien @Noah-s , on fait au mieux.

Bon travail.