Exercice études convergence d'une série [ Besoin d'aide ]
-
Robz dernière édition par Robz
Bonjour, pourriez vous m'aider, je ne comprends pas du tout l'exercice de ce devoir qui est largement plus dure de ce qui a était fait en cours. En vous remerciant
- Pour tout n ∈ N, on pose P(n) = n² + 3n + 1.
a) Déterminer trois réels (a, b, c) ∈ R^3 tels que ∀n ⩾ 2, P(n) = an(n − 1) + bn + c.
b) Déterminer la nature de la série X et préciser la valeur de sa somme si elle converge.
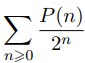
c) Déterminer la nature de la série et préciser la valeur de sa somme si elle converge.
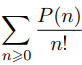
- Pour tout n ∈ N, on pose P(n) = n² + 3n + 1.
-
@Robz Bonjour,
Pour la question a), développe P(n)P(n)P(n) et identifie termes à termes avec l'expression du polynôme initial.
-
Robz dernière édition par
@Noemi Bonjour et merci de ta réponse. Alors j'ai développer P(n) = an^2-na+nb+c mais je n'ai pas compris ce que je doit faire ensuite.
-
Tu identifies chaque terme selon la puissance de nnn :
an2=n2an^2= n^2an2=n2
(−a+b)n=3n(-a+b)n= 3n(−a+b)n=3n
c=1c= 1c=1
puis tu résous ce système.
-
Robz dernière édition par
@Noemi j'ai donc trouvé a=1 et b=4 et ( comment avez vous trouvé c=2)
-
@Robz
Une erreur de frappe pour ccc, que j'ai rectifiée.