fonction exponentielle

[Maeeee]

Bonjour, est ce que quelqu'un pourrait m'aider et m'expliquer la démarche à suivre ? Je reste bloquée à la première question. Je trouve que f=u*v= u'v+v'u avec u=( x² -2,5x +1) , u'= 2x-2,5 , v=e^x et v'= e^x
Seulement, je n'arrive pas a simplifier f'(x). Merci pour votre aide.

Soit f la fonction définie sur R par :
f (x) = (x²– 2,5x + 1)e^x
Voici sa courbe représentative:

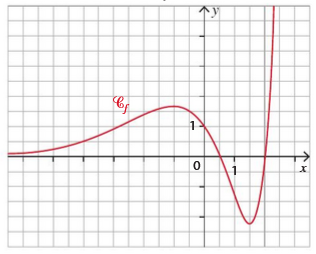
On note f ' la fonction dérivée de f.
a. Calculer f '(x).
b. Étudier le signe de f '(x) sur son domaine de définition.
c. Dresser le tableau de variation de la fonction f sur R.
La tangente à Cf au point A d’abscisse –1 recoupe
la courbe Cf au point M.
Déterminer à la calculatrice une valeur approchée de
l’abscisse de M (expliquer la démarche).
Déterminer une équation de la tangente T à la
courbe Cf au point B d’abscisse 0.
Compléter la fonction en Python ci-dessous afin
qu’elle permette d’approcher, au dixième près, l’abscisse du point P intersection de la tangente T et de Cf.

Scan supprimé par la modération du site.

[mtschoon]

@Maeeee , bonjour,

Comme la modération te l'a dit dans un autre topic, ici, les énoncés doivent être écrits et non scannés.
Les énoncés scannés sont supprimés (par la modération)

voir :
https://forum.mathforu.com/topic/33745/fonction-exponentielle

Je te réponds donc à la question écrite à la main:
$f(x)=(x^2–2,5x+1)e^x$
Calcul de $f^{\prime }(x)$

Ce que tu as indiqué est exact

cela te donne :
$f^{\prime }(x)=(2x-2.5)e^x+(x^2-2.5x+1)e^x$

Tu mets $e^x$en facteur :
$f^{\prime }(x)=e^x(2x-2.5+x^2-2.5x+1)$

$f^{\prime }(x)=e^x(x^2-0.5x-1.5)$

Tu peux factoriser le second facteur qui est un polynôme du second degré.
$x^2-0.5x-1.5=0$, après calculs, a pour solutions $x_1=-1$ et $x_2=1.5$
donc :$x^2-0.5x-0.5=(x-x_1)(x-x_2)$
$x^2-0.5x-0.5=(x+1)(x-1.5)$

donc :
$\boxed{f^{\prime }(x)=e^x(x+1)(x-1.5)}$

[mtschoon]

@Maeeee ,

Tu t'es peut-être trompé(e) de rubrique car la fonction exponentielle, en principe, ne s'étudie pas en classe de Première...Bizarre...

[mtschoon]

Bonsoir,
Je suppose que la modération supprimera tes parties d'énoncé scannées si tu ne les supprimes pas toi même, @Maeeee .

Je ne t'ai répondu qu'à la partie non scannée (simplification de $f^{\prime }(x)$)