ÉQUATION DU SECOND DEGRÉ ET THÉORÈME DE PYTHAGORE (URGENT)
-
Lou able dernière édition par
Bonjour, étant en classe de seconde, j'ai un dm à réaliser, or je n'étais pas là la semaine du cours, donc je ne vois pas comment faire
voici l'énoncé de l'exercice qui me pose problème:
Soit ABCD un rectangle, E le milieu de [BC] et le point de [BA] tel que BF= 1/4 AB
Déterminer les dimensions du rectangle ABCD pour que le triangle DEF soit un triangle rectangleJe remercie d'avance tout celles et ceux qui me proposeront une quelconque aide de leur part en utilisant un peu de leur temps, une explication ou juste une ébauche pour savoir par où commencer, vraiment n'importe quoi.
Merci beaucoup pour votre attention
-
mtschoon dernière édition par mtschoon

@Lou-able , bonjour,
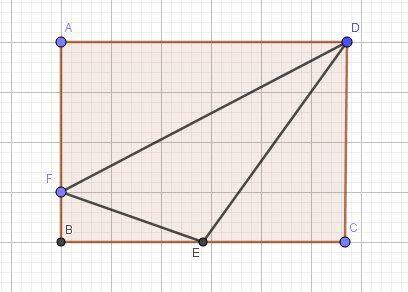
Quelques pistes possibles,
Soit AB=xAB=xAB=x et BC=yBC=yBC=y avec x≤yx\le yx≤y
BE=EC=y2BE=EC=\dfrac{y}{2}BE=EC=2y
BF=x4BF=\dfrac{x}{4}BF=4x ; AF=3x4AF=\dfrac{3x}{4}AF=43x
Utilise 3 fois les théorèmes de Pythagore :
EF2=BE2+BF2EF^2=BE^2+BF^2EF2=BE2+BF2
ED2=EC2+CD2ED^2=EC^2+CD^2ED2=EC2+CD2
DF2=FA2+AD2DF^2=FA^2+AD^2DF2=FA2+AD2Tu obtiendras ainsi les expressions de EF2,ED2,DF2EF^2,ED^2,DF^2EF2,ED2,DF2 en fonction de xxx et yyy.
DEFDEFDEF triangle rectangle (en EEE) , avec la réciproque du Théorème de Pythagore, te permet d'écrire :
DF2=EF2+ED2DF^2=EF^2+ED^2DF2=EF2+ED2Cette égalité te donnera ainsi une équation d'inconnues xxx et yyy
En mettant les termes en xxx dans un membre et les termes en yyy dans l'autre , après simplification, tu dois obtenir, sauf erreur : x2=y2x^2=y^2x2=y2xxx et yyy sont des longueurs donc positives, donc tu peux déduire x=y\boxed{x=y}x=y
Conclusion : le rectangle ABCD est un carré (longueur et largeur égales).
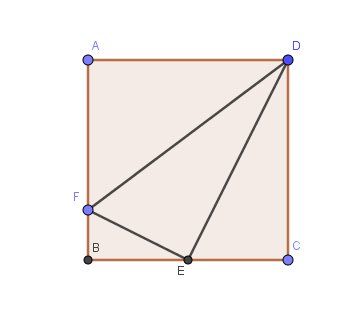
Bons calculs .
-
Lou able dernière édition par
@mtschoon , Bonjour merci beaucoup, je ne savais pas comment utiliser les égalités dans ce cas sans savoir quel sommet était carré, ça m'avance beaucoup, merci encore
-
Lou able dernière édition par
@mtschoon , rebonjour, je me permets de vous recontacter car, j'ai fait plusieurs calcul, j'ai déjà essayé de calculer les égalités en partant du principe que ABCD est un carré, mais j'ai trouvé que CD= 0,75x ce qui est impossible puisque CD= x , donc j'ai essayé de trouver le résultat avec les autres égalités que l'on peut trouver avec les autres triangles rectangles non évoqués dans l'énoncé, mais là encore je n'ai pas trouvé car l'hypoténuse, [DF], le résultat de son carré ne correspond pas à la somme des deux autres cotés au carrés,
Je m'excuse encore une fois de prendre de votre temps, mais j'espère que vous aurez l'amabilité de me répondre si vous en avez la possibilité, merci beaucoup.
-
mtschoon dernière édition par mtschoon

Tu n'as pas à partir du principe que ABCD est un carré , vu que c'est la conclusion.
Tu pars du principe que ABCD est un rectangle.Dans ma proposition, j'ai supposé que ABCD était un rectangle avec x≤yx \le yx≤y (mais rien n'était indiqué dans ton énoncé donné.)
Fais tranquillement tes calculs,
Sauf erreur, tu dois trouver, en réduisant au même dénominateur
EF2=4y2+x216EF^2=\dfrac{4y^2+x^2}{16}EF2=164y2+x2
ED2=4y2+16x216ED^2=\dfrac{4y^2+16x^2}{16}ED2=164y2+16x2
FD2=9x2+16y216FD^2=\dfrac{9x^2+16y^2}{16}FD2=169x2+16y2