equation de droite / mediatrice .....

salut jai un gros probleme sur un exercice je ne sais pas du tout par ou commencer si quelqun pourrait maider sil vous plait
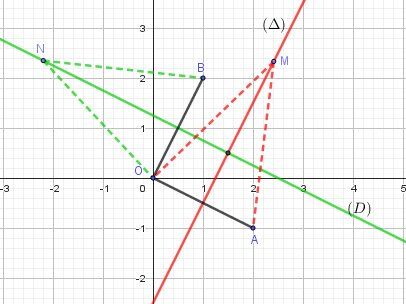
au moins mexpliquer comment faire je nyncomprend rien

dans un repere orthonorme ( o;i;j) on considere les point A(2; -1) B ( 1; 2 ) et M (x ; y )

exprimer MO au carre et MA au carre en fonction de x et y
on rappelle que la mediatrice delta de [OA] est lensemble des points M tels que MO= MA
Comme ce distances sont positive cela revient a MO au carre ) MA au carre
en deduire une equation cartesienne de delta
de meme determiner une equatiopn cartesienne de la mediatrice [OB] notee d

@timmmm , bonjour,

Schéma pour éclairer,

médiatrices.jpg

@mtschoon mais je comprend pas comment exprimer ya des formule ? ou autre

@timmmm , Pistes pour les calculs,

Regarde ton cours pour la formule de la distance,

$O (0, 0)$
$M (x, y)$

$MO^2=(x_O-x_M)^2+(y_O-y_M)^2$
$MO^2=(0-x)^2+(0-y)^2$
$MO^2=(-x)^2+(-y)^2$
$MO^2=x^2+y^2$

Tu fais pareil pour $MA^2$

$A (2, - 1)$
$M (x, y)$

$MA^2=(x_A-x_M)^2+(y_A-y_M)^2$
$MA^2=(2-x)^2+(-1-y)^2$
Tu développes avec les identités remarquables et tu simplifies.

Sauf erreur, après calculs, tu dois trouver :
$MA^2=x^2-4x+y^2+2y+5$

En écrivant l'égalité $MO^2= MA^2$ , tu obtiendras l'équation de $(Δ)(\Delta)$ médiatrice de $[O A]$

Même principe pour $(D)$ médiatrice de $[O B]$

Tu peux donner tes résultats si tu souhaites une vérification.

@mtschoon dans mon cours il ny a pas de formule de distance elle sert a quoi dans ce cas

aussi quest ce que la mediatrice mon cours nen fait pas reference non plus

@timmmm , la médiatrice d'un segment est l'ensemble de points équidistants des extrémités de ce segment.

$(Δ)(\Delta)$ médiatrice de $[O A]$ est l'ensemble des points $M$ tels que $M O = M A$ c'est à dire, en élevant au carré :
$MO^2=MA^2$
(C'est marqué dans ton énoncé)

Pour la formule de la distance entre deux points dont on connait les coordonnées, tu peux regarder ici, si besoin ( mais elle doit être quelque part dans ton cours de Seconde ou avant...)

FORMULE (dans un repère orthonormé du plan)
https://lexique.netmath.ca/distance-entre-deux-points-dans-le-plan-cartesien/

Entre deux points $I(x_1,y_1)$ et $J(x_2,y_2)$ ,

$IJ=(x2−x1)2+(y2−y1)2IJ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
En élevant au carré, on a donc (ce que tu dois faire dans ton exercice) :
$IJ^2=(x_2-x_1)^2+(y_2-y_1)^2$

@mtschoon mais pourquoi jai besoin de connaitre la distance entre deux point pour une equatoin cartessienne je suis un peu perdu ...

@timmmm , relis tranquillement tout ce que je t'ai indiqué.
Il y a tout le nécessaire.

Prends le temps qu'il faut pour comprendre.

Je viens , à l'instant, de taper les indications que tu demandais (vu que tu semblais en avoir besoin) ... donc tu n'a pas eu le temps de réfléchir...

Pour la deuxième question, lorsque tu auras calculé $MO^2$ et $MA^2$ (première question) , comme indiqué, en écrivant $MO^2=MA^2$ , tu obtiendras l'égalité :

$x^2+y^2=x^2-4x+y^2+2y+5$

En simplifiant, en transformant , tu obtiendras l'équation de la droite $(Δ)(\Delta)$ .
Tu dois obtenir, sauf erreur, $4 x - 2 y - 5 = 0$ c'est à dire $y=2x−52y=2x-\dfrac{5}{2}$

Lorsque tu auras compris , tu pourras appliquer le même principe pour la médiatrice de $[O B]$

Ce message a été supprimé !

@mtschoon je ne sais pas comment retirer les ² cest ici ou je dois utiliser la formule ?

@timmmm , tu simplifies , tout simplement :
$x^2+y^2=x^2-4x+y^2+2y+5$
Tu pourrais barrer directement ...

sinon, en transposant :

$x^2+y^2-x^2+4x-y^2-2y-5=0$

$x^2-x^2=0$
$y^2-y^2=0$
Il reste : $4 x - 2 y - 5 = 0$

@mtschoon
ok ducoup jappliqu la meme choses sur OB
donc OB + MO+BM
BM²= ( xm - xb)² + (ym - yb)
BM²= (x-1)² = (y- 2)²
BM² = x² -x - x +1+y²-2y-2Y + 4
BM²= x²-2x +y²-4y+5
cest ca je crois ?
ensuitye vue que jia pas legaliotee de tout a l heure MO+MA jai le droit quand meme de faire = 0?

@timmmm ,

Dans mon schéma, j'ai appelé $N (x, y)$ un point quelconque de la médiatrice de $[O B]$ mais tu peux l'appeler $M$ si tu préfères.

Fais attention : il y a des confusions entre + et =
$BM^2= (x-1)^2+ (y- 2)^2$

C'est bon pour $BM^2=x^2-2x+y^2-4y+5$

Ensuite, tu appliques la logique habituelle.
$MO^2=MB^2$

Tu continues avec la méthode vue précédemment.

@mtschoon ok donc juste pour verifie notre equation cartesienne de OB cest bien 2x+4y+5 =0 ?

aussi apres on me demande les coordonee de c qui est le point dintersection entre ces deux droites
jai fait :

xc = xb + xo / 2
et
yc = yb + yo / 2

soit xc= 1+0/2 = 1/2 =1
yc= 2+ 0 / 2 = 2/2 = 0,5 c(1;0,5)

est ce la bonne methode ? et est ce que c bon sur votre schema je nai pas limpression que se soit bon

@timmmm , il y a une erreur de signe dans l'équation de la médiatrice de $[O B]$

Vérifie.

@mtschoon -2x - 4y +5 ?

et pour le schema il me rest eune question jai reussi les calcules mais je pense suil son faux

@timmmm , l'équation de la médiatrice de $[O B]$ , peut être écrite $- 2 x - 4 y + 5 = 0$ ou si tu préfères $2 x + 4 y - 5 = 0$

Pour trouver les coordonnées de $C$ intersection des deux droites, tu dois résoudre le système composé par les deux équations obtenues :
${4x−2y−5=0−2x−4y+5=0\begin{cases}4x-2y-5=0\cr -2x - 4y +5 =0\end{cases}$

Tu utilises la méthode de ton choix .

Je te mets un lien vers le programme de Troisième ici :
https://www.mathforu.com/troisieme/resolution-de-systemes-d-equations/

Après calculs, tu dois trouver, pour les coordonnées de $C$ : $12)\biggr(\dfrac{3}{2}\ ,\ \dfrac{1}{2}\biggr)$

Bons calculs.

@mtschoon ok pour c javais bon et derniere question
comment je peut connaitre la nature avec un point k millieu de AB est cer que je dois simplement me fiee au schema et mettre la nature ?

@timmmm , je ne comprends pas de quoi du parles..
De quelle nature s'agit-il ? ? ?

En ce qui concerne les coordonnées de $K$ milieu de $[A B]$
$xK=xA+xB2x_K=\dfrac{x_A+x_B}{2}$
$yK=yA+yB2y_K=\dfrac{y_A+y_B}{2}$

@mtschoon deja k jai trouver k(1,5;0,5)

ensuite il me demande den deduire la nature du triangle OAB
ducouc dois je me fiee a votre schema ?

@timmmm ,

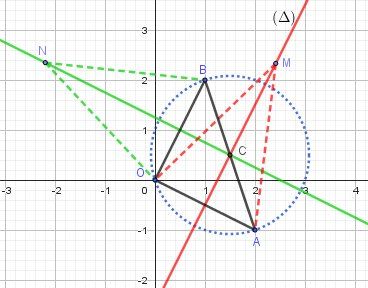
$K$ est confondu avec $C$ (mêmes coordonnées)
Donc $C$ est le milieu de $[A B]$

Le schéma permet de conjecturer, vérifier, mais il faut prouver.

Le triangle $O A B$ parait être rectangle-isocèle mais il faut faire les démonstrations.

@mtschoon et comment je suis cense faire ? avec les proprietee du triangle ?

@timmmm ,

Pour démontrer que $O A = O B$ tu peux utiliser la formule de la distance de deux points donc triangle isocèle

Pour démontrer que l'angle $AOB^\widehat{AOB}$ est droit , tu peux raisonner.

Avec la propriété relative aux médiatrices (utilisée dans cet exercice) $C O = C A = C B$

Le cercle de centre $C$ et de rayon $C O$ passe par $A$ et $B$ .
$[A B]$ est un diamètre de ce cercle.
Par théorème, lorsqu'on joint un point d'un cercle (autre que $A$ et $B$ ) aux extrémités d'un diamètre $[A B]$ , on forme un angle droit,donc triangle rectangle.

@mtschoon donc en conclusion le triangle est rectangle vue que ca passe par a et b ?

@timmmm ,
Ta phrase n'est pas très claire, mais le triangle est bien rectangle
.

@mtschoon ok merci infiniment vous mavez sauvez et normalement je devrait reussir mon controle demain encore merci

De rien @timmmm , bon contrôle pour demain, et surtout fais bien attention aux explications/rédaction.