arbre pondéré valide ou non?

Bonjour,
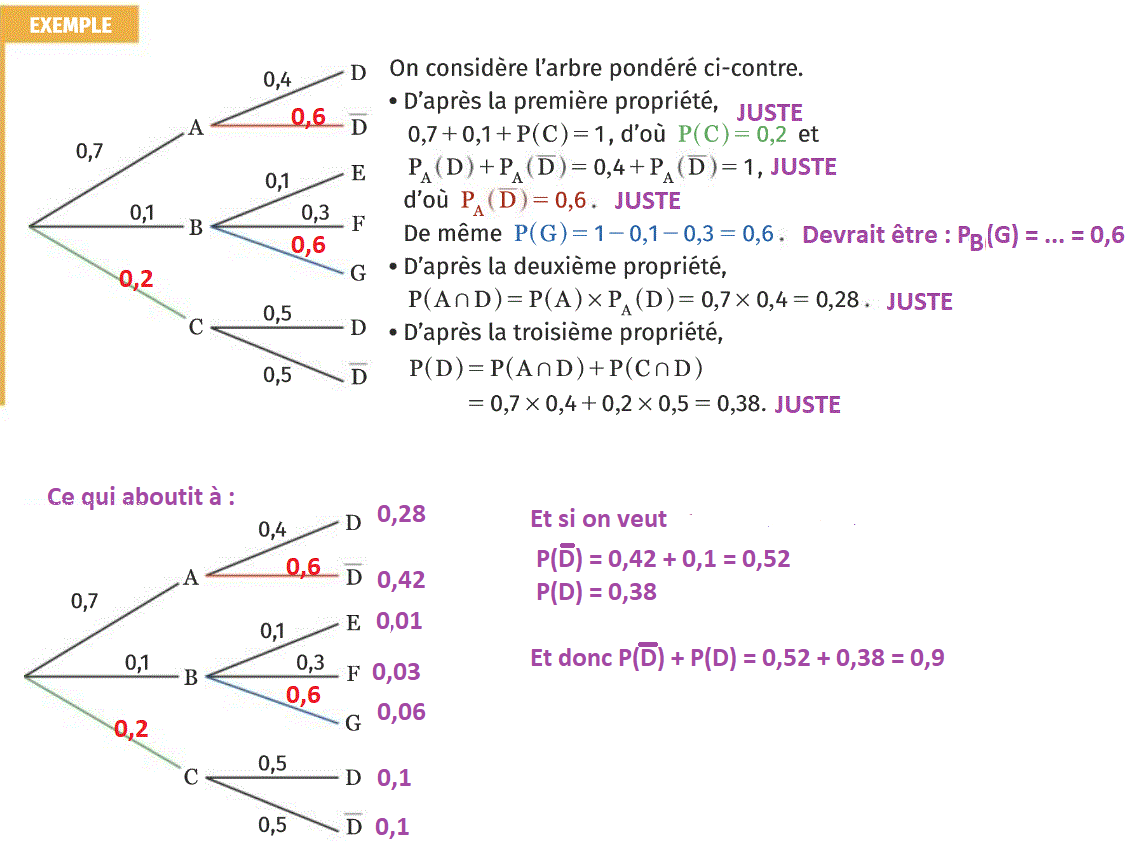
j'ai un sérieux doute sur la validité de l'arbre pondéré, dans l'exemple à la fin de la page 286 de ce manuel :
https://www.calameo.com/read/000596729923535cd3427

En essayant d’exposer le problème par le calcul :
P(D barre) = P(D barre inter A) + P(D barre inter C)
P(D barre) = P(D barre sachant A) * P(A) + P(D barre sachant C) * P(C)
P(D barre) = 0.6 * 0.7 + 0.5 * 0.2
P(D barre) = 0.42 + 0.1 = 0.52
Or, P(D) = 0.38
Donc P(D) + P(D barre) = 0.9 …

Qu’en pensez-vous ?

@Marie_Sophie

Bonjour,

Tu as posé la même question sur d'autres sites ... Et tu as reçu des réponses, par exemple ici :

https://www.bibmath.net/forums/viewtopic.php?id=16123

Bonjour,

@Marie_Sophie , comme te l'a indiqué @Black-Jack , tu as posé la même question sur plusieurs sites.

Tu as donc fait du "multipost", ce qui n'est pas autorisé.

Regarde les consignes avant de poster :
https://forum.mathforu.com/topic/1383/stop-lire-ce-sujet-tu-devras-avant-de-poster-ton-message

Alors, tu ne devrais pas avoir de réponse ici , mais comme ta question est vraiment très pertinente, contrairement à mes habitudes, je vais regarder de quoi il s'agit, car ça m'interpelle.

Je viens de regarder :
Effectivement, l'arbre dont tu parles n'est exact qu'en apparence !
Si l'on fait les calculs, il est FAUX.
Celui qui l'a écrit s'est visiblement contenté des apparences....

Si tu veux t'entraîner, tu peux essayer de faire les modifications pour rendre cet arbre cohérent.

@mtschoon Merci !!

@mtschoon a dit dans arbre pondéré valide ou non? :

Bonjour,

@Marie_Sophie , comme te l'a indiqué @Black-Jack , tu as posé la même question sur plusieurs sites.

Tu as donc fait du "multipost", ce qui n'est pas autorisé.

Regarde les consignes avant de poster :
https://forum.mathforu.com/topic/1383/stop-lire-ce-sujet-tu-devras-avant-de-poster-ton-message

Alors, tu ne devrais pas avoir de réponse ici , mais comme ta question est vraiment très pertinente, contrairement à mes habitudes, je vais regarder de qui il s'agit, car ça m'interpelle.

Je viens de regarder :
Effectivement, l'arbre dont tu parles n'exact qu'en apparence !
Si l'on fait les calculs, il est FAUX.
Celui qui l'a écrit s'est visiblement contenté des apparences....

Si tu veux t'entraîner, tu peux essayer de faire les modifications pour rendre cet arbre cohérent.

Bonjour,

Je serais content de voir ce qui est faux (si ce n'est un petit B oublié dans une ligne.

Tout n'est évidemment pas calculé sur le site, mais ce qui est indiqué (à part le petit B oublié) me semble correct.

Sans titre.png

Me trompe-je ?

Bonjour,

Ce qu'il y a peut-être de non habituel est de noter par exemple D et D(barre) avec D + D(barre) différent de 1, mais cela reste quant même parfaitement compréhensible.

On a 5 issues possibles qui sont D, D(barre), E, F et G (avec D+D(barre) différent de 1)
C'eut été plus "conventionnel" de noter D et D(barre) de 2 lettres différentes.

@Black-Jack
Bonjour Black Jack,
par définition, Dbarre, l’événement contraire de D, contient toutes les issues de Omega qui ne sont pas dans D.
Donc D union Dbarre = Omega, et p(D) + P(Dbarre) = 1.
N’est-ce pas ?

@Marie_Sophie

@Marie_Sophie a dit dans arbre pondéré valide ou non? :

par définition, Dbarre, l’événement contraire de D, contient toutes les issues de Omega qui ne sont pas dans D.
Donc D union Dbarre = Omega, et p(D) + P(Dbarre) = 1.
N’est-ce pas ?

@Marie_Sophie , je confirme.

Voir lien :
https://college-montaigne.fr/wp-content/uploads/maths/310 - Probabilités - Qu'est-ce qu'un événement contraire.pdf

Bonjour,

Il y a (comme je l'ai écrit ailleurs) une "indélicatesse dans l'écriture de l'arbre.

Il aurait été beaucoup moins litigieux de noter l'issue D(barre) par une autre lettre (par exemple H)

Il y a ici confusion entre P(D) + P(D(barre)) et PA(D) + PA(D(barre).

Le site a noté PA(D) + PA(D(barre) = 1 ... et c'est juste.

Il n'a nul part noté P(D) + P(D(barre)) = 1

Le quiproquo n'aurait pas été possible en notant H au lieu de D(barre).

Comme souvent, il y a plusieurs interprétations possibles.

Voir par exemple le message 3 sur l'autre site, il est dans le même point de vue que moi.

Il reste évidemment toujours "dangereux" et pas recommandé de noter le D et D(barre) comme sur l'arbre de l'exercice.

@Black-Jack
Je n’ai pas confondu P(D sachant A) + P(Dbarre sachant A) avec P(D) + P(Dbarre).

Même si ce manuel ne mentionne pas que P(D) + P(Dbarre) = 1, c’est vrai quel que soit l’événement D, à cause de la définition même de Dbarre. Et toute hypothèse qui implique P(D) + P(Dbarre) différent de 1 est une hypothèse fausse (raisonnement par l’absurde).

Re-bonjour,
@Marie_Sophie a dit dans arbre pondéré valide ou non? :

@Black-Jack
Je n’ai pas confondu P(D sachant A) + P(Dbarre sachant A) avec P(D) + P(Dbarre).

Même si ce manuel ne mentionne pas que P(D) + P(Dbarre) = 1, c’est vrai quel que soit l’événement D, à cause de la définition même de Dbarre. Et toute hypothèse qui implique P(D) + P(Dbarre) différent de 1 est une hypothèse fausse (raisonnement par l’absurde).

Je suis 1000 fois d'accord avec toi @Marie_Sophie et tu n'as rien confondu du tout...

(Si tu es une élève de Première, tu es une "Super-élève" et si par hasard tu es prof (ou autre...), tu as vraiment raison d'être choquée..., je le suis aussi.

Un manuel (?) ou site (?) pour des élèves de Première , qui met un exemple d'arbre probabiliste avec un telle erreur est à proscrire ! ! !

Si celui qui a fait cet arbre avait un peu réfléchi et si il était un peu matheux, il aurait bien vu que, même sans faire les calculs, $p(D)+p(D‾)=p(A)+p(C)p(D)+p(\overline{D})=p(A)+p(C)$ , donc forcément $0.9\boxed{0.9}$ , vu que $p (B)$ vaut $0.1$ .
Donc l'arbre donné sur le site est FAUX.

A la question de ton titre "arbre pondéré valide ou non?" je répondrais , sans l'ombre d'un doute, "non valide"

Bien sûr, comme dit @Black-Jack, la grossière erreur est de parler d'évènement contraire de $D$ de cette façon !
Il fallait, par exemple, prendre deux évènements $I$ et $J$ , et faire un arbre de ce type :

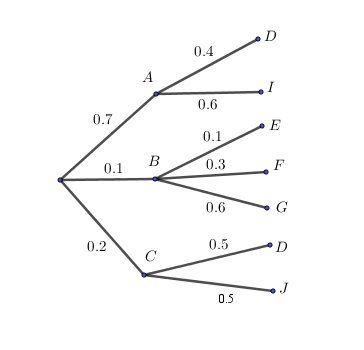
Ainsi :
$p(D)=(0.7×0.4)+(0.2×0.5)=0.38p(D)=(0.7\times 0.4)+(0.2\times 0.5)=0.38$
Par définition/théorème : $p(D‾)=1−0.38=0.62p(\overline D)=1-0.38=0.62$

On peut vérifier ce résultat en calculant avec les autres branches :
$p(D‾)=(0.7×0.6)+(0.1×0.1)+(0.1×0.3)+(0.1×0.6)+(0.2×0.5)=0.62p(\overline D)=(0.7\times 0.6)+(0.1\times 0.1)+(0.1\times 0.3)+(0.1\times 0.6)+(0.2\times 0.5)=0.62$

CQFD.

Ce message a été supprimé !

@mtschoon Merci pour votre appréciation ! Je suis une amie d'une élève de 1ère, j'ai une prédilection pour les maths et je l'aide ... elle n'a pas le temps de poser toutes les questions qu'elle voudrait sur les forums.
En examinant cet arbre, en essayant de lui donner des indications pour s'assurer que ses arbres soient valides, je me suis aperçue que celui-ci avait un problème ... rien de tel pour embrouiller les élèves qui peuvent croire le manuel inerrant !
Errare humanum est, sed perseverare diabolicum; même les profs et auteurs de manuels peuvent faire des erreurs, mais il faut pouvoir les leur signaler et qu'ils puissent les corriger ...
Ce qui rend ce manuel pratique: il est en ligne ...
Quels sont les meilleurs manuels à votre avis?

On m'a fait remarquer que si on admet que D est incompatible avec E, F et G, et que la réunion de tous les événements en bout d'arbre forme Omega, alors Dbarre = E union F union G, et on peut transformer l'arbre en ne faisant partir qu'une seule branche de B allant vers Dbarre, avec P(Dbarre sachant B) = 1; l'arbre ainsi obtenu permet d'appliquer les règles de calcul propres aux arbres de probabilités. C'est vrai, mais même si l'énoncé disait que D est incompatible avec E, F et G, l'arbre à la fin de la page 286 n'en deviendrait pas valide pour autant ; d'après ce que je comprends, pour qu’un arbre de probabilités soit valide, il faut que l’on puisse lui appliquer directement les règles de calcul listées sur cette même page 286, en particulier :
« la probabilité d’un événement est égale à la somme des probabilités des chemins conduisant à cet événement ».
Cette règle ne dit pas :
« la probabilité d’un événement A est égale à la somme des probabilités des chemins conduisant à cet événement A et des chemins conduisant à tout événement inclus dans A ».

Même si cette donnée supplémentaire figurait dans l’énoncé, l’arbre tracé dans ce manuel à la fin de la page 286 ne permettrait toujours pas l’application directe des règles de calcul propres aux arbres de probabilités, et de ce fait, ne serait pas valide, à mon avis.

Un arbre de probabilités est une représentation graphique formelle qui doit satisfaire certaines conditions permettant des calculs clairs et sans ambiguïté. On ne doit pas avoir à se demander, pour les événements en bout d’arbre : «est-ce que j’ai des morceaux de Dbarre disséminés dans les autres événements» ?

Et justement, j’étais en train d’essayer de clarifier des conditions à remplir (qui ne figurent pas dans ce manuel) pour qu’un arbre de probabilités soit valide, et permette d’appliquer directement les règles de calcul listées dans ce manuel.

Il me semble que l’une de ces conditions, c’est que tous les événements en bout d’arbre doivent être, 2 à 2, soit incompatibles, soit identiques. Et que ceux qui sont incompatibles doivent former une partition de Omega. Qu’en pensez-vous ? Il existe sûrement de bons manuels sur les probabilités / graphes, expliquant tout cela …

@Marie_Sophie , bonjour,

C’est gentil à toi de donner des précisions. Je me doutais que tu n’étais pas élève de Première ...

Ton amie a de la chance que tu l’aides !

Les arbres probabilistes sont la traduction graphique des démarches probabilistes.

Avant l’usage des arbres, il fallait écrire des lignes de formules avec évenements, évenements contraires, intersections, unions, probabilités, c’était très lourd.
Pour les élèves, l’utilisation d’un arbre est plus clair et plus simple.

Je n’ai pas d’indication de manuels précis à proposer.

Je te joins deux documents (tu les as déjà peut-être consultés) sur les arbres probabilistes.

https://irem.univ-poitiers.fr/portail/attachments/article/144/arbres_probabilistes.pdf

https://www.apmep.fr/IMG/pdf/Arbre_Parzysz_.pdf

Bonne journée et peut-être à une autre fois