Système d’équations olympiades de maths
-
Ccesaire dernière édition par
Trouver tous les couples (x,y)tels que
x+y^2=y^3
y+x^2=x^3
-
BBlack-Jack dernière édition par
Bonjour,
Une possibilité ... un peu longue, il y a sûrement beaucoup plus direct si on trouve l'astuce.
x+y²=y³ ---> x = y³-y²
y+x²=x³y + (y³-y²)² = (y³-y²)²
On développe ... et on arrive à : y9−3y8+3y7−2y6+2y5−y4−y=0y^9-3y^8+3y^7-2y^6+2y^5-y^4-y=0y9−3y8+3y7−2y6+2y5−y4−y=0donc : y.(y8−3y7+3y6−2y5+2y3−y3−1)=0y.(y^8-3y^7+3y^6-2y^5+2y^3-y^3-1)=0y.(y8−3y7+3y6−2y5+2y3−y3−1)=0
Si on suppose x = y, on aurait y+y²=y³
y(y²-y-1)=0
Et donc y.(y8−3y7+3y6−2y5+2y3−y3−1)y.(y^8-3y^7+3y^6-2y^5+2y^3-y^3-1)y.(y8−3y7+3y6−2y5+2y3−y3−1) est divisible par y2−y−1y^2-y-1y2−y−1
On fait la division euclidienne et on trouve :
y.(y2−y−1).(y6−2y5+2y4−2y3+2y2−y−1)=0y.(y^2-y-1).(y^6-2y^5+2y^4-2y^3+2y^2-y-1)=0y.(y2−y−1).(y6−2y5+2y4−2y3+2y2−y−1)=0on a donc des solutions :
y = 0 (et x = 0)
de y²-y-1 = 0, on a y=1+52y=\frac{1+\sqrt{5}}{2}y=21+5 (... qui donne x=1+52x=\frac{1+\sqrt{5}}{2}x=21+5)
et on a aussi : y=1−52y=\frac{1-\sqrt{5}}{2}y=21−5 (... qui donne x=1−52x=\frac{1-\sqrt{5}}{2}x=21−5)Il reste des solutions éventuelles à partir de : (y6−2y5+2y4−2y3+2y2−y−1)=0(y^6-2y^5+2y^4-2y^3+2y^2-y-1)=0(y6−2y5+2y4−2y3+2y2−y−1)=0
On étudie les variations de f(y)=y6−2y5+2y4−2y3+2y2−y−1f(y) = y^6-2y^5+2y^4-2y^3+2y^2-y-1f(y)=y6−2y5+2y4−2y3+2y2−y−1
f'(y) = ...
f''(y) = ... et on trouve que f''(y) > 0 sur R et donc f'(y) est strictement croissante.
on montre que f'(y) = 0 pour une seule valeur de y ... qui correspond au minimum de f(y) et que ce minimum est > 0
Donc f(y) = 0 n'a pas de solutions réelles.Les solutions aux problèmes sont donc les couples(0,0)(0 , 0)(0,0) , (1+52;1+52)(\frac{1+\sqrt{5}}{2};\frac{1+\sqrt{5}}{2})(21+5;21+5) et (1−52;1−52)(\frac{1-\sqrt{5}}{2};\frac{1-\sqrt{5}}{2})(21−5;21−5)
... Sauf si je me suis trompé quelque part. (ce qui est bien possible)
Et (déjà dit), il y a sûrement plus court pour arriver au but.
-
Ccesaire dernière édition par
@Black-Jack merci. Tu me sauve. J’enverrai d’autres exercices de ce type
-
mtschoon dernière édition par mtschoon

Bonjour,
Une alternative,
Si l'on observe ce système, xxx d'une équation s'échange avec yyy de l'autre( est vice versa)
Soit (α,β)(\alpha,\beta)(α,β) le couple-solution d'une équation.
Le couple (β,α)(\beta,\alpha)(β,α) sera solution de l'autre.Ainsi, les couples solutions du système devront satisfaire à (α,β)=(β,α)(\alpha,\beta)=(\beta,\alpha)(α,β)=(β,α) , c'est à dire α=β\alpha=\betaα=β
Ils seront de la forme (α,α)(\alpha,\alpha)(α,α)α+α2=α3\alpha+\alpha^2=\alpha^3α+α2=α3 <=>α3−α2−α=0\alpha^3-\alpha^2-\alpha=0α3−α2−α=0
c'est à dire : α(α2−α−1)=0\alpha(\alpha^2-\alpha-1)=0α(α2−α−1)=0
α=0\alpha=0α=0 ou (α2−α−1)=0(\alpha^2-\alpha-1)=0(α2−α−1)=0
(α2−α−1)=0(\alpha^2-\alpha-1)=0(α2−α−1)=0 <=>α=1+52\alpha=\dfrac{1+\sqrt 5}{2}α=21+5 ou α=1−52\alpha=\dfrac{1-\sqrt 5}{2}α=21−5Conclusion : les couples solutions sont :
(0,0),(1+52,1+52),(1−52,1−52)(0,0),(\dfrac{1+\sqrt 5}{2},\dfrac{1+\sqrt 5}{2}), (\dfrac{1-\sqrt 5}{2},\dfrac{1-\sqrt 5}{2})(0,0),(21+5,21+5),(21−5,21−5)
-
BBlack-Jack dernière édition par
@mtschoon a dit dans Système d’équations olympiades de maths :
Bonjour,
Une alternative,
Si l'on observe ce système, xxx d'une équation s'échange avec yyy de l'autre( est vice versa)
Soit (α,β)(\alpha,\beta)(α,β) le couple-solution d'une équation.
Le couple (β,α)(\beta,\alpha)(β,α) sera solution de l'autre.Ainsi, les couples solutions du système devront satisfaire à (α,β)=(β,α)(\alpha,\beta)=(\beta,\alpha)(α,β)=(β,α) , c'est à dire α=β\alpha=\betaα=β
Ils seront de la forme (α,α)(\alpha,\alpha)(α,α)α+α2=α3\alpha+\alpha^2=\alpha^3α+α2=α3 <=>α3−α2−α=0\alpha^3-\alpha^2-\alpha=0α3−α2−α=0
c'est à dire : α(α2−α−1)=0\alpha(\alpha^2-\alpha-1)=0α(α2−α−1)=0
α=0\alpha=0α=0 ou (α2−α−1)=0(\alpha^2-\alpha-1)=0(α2−α−1)=0
(α2−α−1)=0(\alpha^2-\alpha-1)=0(α2−α−1)=0 <=>α=1+52\alpha=\dfrac{1+\sqrt 5}{2}α=21+5 ou α=1−52\alpha=\dfrac{1-\sqrt 5}{2}α=21−5Conclusion : les couples solutions sont :
(0,0),(1+52,1+52),(1−52,1−52)(0,0),(\dfrac{1+\sqrt 5}{2},\dfrac{1+\sqrt 5}{2}), (\dfrac{1-\sqrt 5}{2},\dfrac{1-\sqrt 5}{2})(0,0),(21+5,21+5),(21−5,21−5)Bonjour,
Je suis, peut être à tort, un peu mal à l'aise avec cette démo.
Si par exemple, le système de départ était :
x² + y^4 = 2y²
y² + x^4 = 2x²Si on fait :
Soit (α,β) le couple-solution d'une équation.
Le couple (β,α) sera solution de l'autre.Ainsi, les couples solutions du système devront satisfaire à (α,β)=(β,α) c'est à dire α=β
Ils seront de la forme (α,α)... ce n'est pas correct, ici par exemple (-1,1) est solution et n'est pas de la forme (α,α)
Me trompe-je ?
-
mtschoon dernière édition par

Rebonjour , bonsoir,
@Black-Jack , dans l'exemple que tu donnes, tous les exposants sont pairs, c'est pour cela que tu peux obtenir des signes ∓\mp∓ et pas forcément α=β\alpha=\betaα=β
-
BBlack-Jack dernière édition par
@mtschoon a dit dans Système d’équations olympiades de maths :
Rebonjour , bonsoir,
@Black-Jack , dans l'exemple que tu donnes, tous les exposants sont pairs, c'est pour cela que tu peux obtenir des signes ∓\mp∓ et pas forcément α=β\alpha=\betaα=β
Bonjour,
Certes.
Le but était de montrer qu'à partir de :
"Soit (α,β) le couple-solution d'une équation.
Le couple (β,α) sera solution de l'autre."... on ne peut conclure de manière générale "Ainsi, les couples solutions du système devront satisfaire à (α,β)=(β,α) c'est à dire α=β, Ils seront de la forme (α,α)"
Evidemment, dans mon exemple, on voit bien que cette conclusion ne peut être faite a priori, dans mon exemple, la raison est évidente, néanmoins, sans démontrer qu'il n'y pas d'autres cas, je reste dubitatif.
Dans ma résolution, c'est démontré par l'étude des variations de f(y)=y^6−2y^5+2y^4−2y^3+2y^2−y−1 ...
Cela complique les choses et il serait bon de trouver la bonne astuce pour s'en dispenser ... mais cela ne peut pas être fait, je pense, par le
"Soit (α,β) le couple-solution d'une équation.
Le couple (β,α) sera solution de l'autre.
Ainsi, les couples solutions du système devront satisfaire à (α,β)=(β,α), c'est à dire α=β\alpha=\betaα=β
Ils seront de la forme (α,α)" ... Sans le justifier (puisque ce n'est pas vrai dans tous les cas)
-
mtschoon dernière édition par mtschoon

Bonjour,
Ces exercices des Olympiades sont « dérangeants »
Le concours français des Olympiades de mathématiques est ouvert aux lycéens volontaires de Première de l’enseignement public et privé sous contrat.
Ce topic aurait dû être posté dans la rubrique Première ( et non Terminale )Seuls ont une chance d’être bien classés à ce concours, les élèves très bons en maths et inventifs.
Ces Olympiades permettent d’aborder « autrement » les problèmes mathématiques.
Il faut donc trouver des solutions « originales » aux problèmes.
Evidemment, @cesaire doit justifier pourquoi cette « astuce » est applicable dans le cas de son énoncé ou en trouver une autre . C’est le but (mais je ne vais pas chercher à sa place...!)
J’ignore quelles sont les intentions de @cesaire
Peut-être qu’il le dira.
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Je ne sais pas ce qui est attendu.
Bonjour,
Pour terminer ...
Autre exemple, le système :
y = x² - 1
x = y² - 1Un des couples solution est (0 , -1), un autre est (-1 , 0)
Les autres sont de la forme (α,α)(\alpha,\alpha)(α,α)
-
mtschoon dernière édition par mtschoon

Bonjour,
Oui effectivement, il faut bien terminer ce topic sans laisser une impression "d'inachevé"
Pour le système d'Olympiades de @cesaire ( qui est le sujet du topic), je mets un schéma d'illustration :
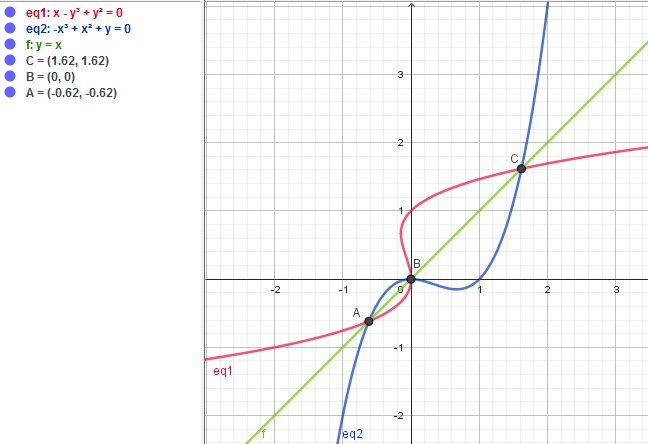
Les solutions du système sont les couples (α,α)(\alpha,\alpha)(α,α), coordonnées des points A,B,C. et il n'y en a pas d'autres.
Un graphique n'est pas une preuve au sens mathématiques.
Il faut justifier par calcul qu'il est impossible qu'il y ait des couples (α,β)(\alpha,\beta)(α,β) solutions avec α≠β\alpha\ne \betaα=β
-
mtschoon dernière édition par mtschoon

Un calcul avec α≠β\alpha\ne \betaα=β
{α+β2=β3β+α2=α3\begin{cases}\alpha+\beta^2=\beta^3\cr \beta+\alpha^2=\alpha^3\end{cases}{α+β2=β3β+α2=α3Par soustraction :
α−β+β2−α2=β3−α3\alpha-\beta+\beta^2-\alpha^2=\beta^3-\alpha^3α−β+β2−α2=β3−α3Identités remarquables :
α−β+(β−α)(β+α)=(β−α)(β2+αβ+α2)\alpha-\beta+(\beta-\alpha)(\beta+\alpha)=(\beta-\alpha)(\beta^2+\alpha\beta+\alpha^2)α−β+(β−α)(β+α)=(β−α)(β2+αβ+α2)Division par (β−α)(\beta-\alpha)(β−α) vu que β−α≠0\boxed{\beta-\alpha\ne 0}β−α=0 et transposition:
−1+β+α−β2−αβ−α2=0-1+\beta+\alpha-\beta^2-\alpha\beta-\alpha^2=0−1+β+α−β2−αβ−α2=0
c'est à dire :
β2+β(α−1)+(α2−α+1)=0\beta^2+\beta(\alpha-1)+(\alpha^2-\alpha+1)=0β2+β(α−1)+(α2−α+1)=0
Equation du second degré d'inconnue β\betaβ, α\alphaα jouant le rôle de paramètre
Δ=(α−1)2−4(α2−α+1)=−3α2+2α−3\Delta=(\alpha-1)^2-4(\alpha^2-\alpha+1)=-3\alpha^2+2\alpha-3Δ=(α−1)2−4(α2−α+1)=−3α2+2α−3
Pour tout α\alphaα réel, Δ<0\Delta\lt 0Δ<0 , donc impossibilité.Bon courage à tout intervenant qui trouverait une autre "astuce".
-
CCandace dernière édition par
In Math Olympiad, problems involving systems of equations often require solving multiple equations simultaneously to find the values of variables. These problems test problem-solving skills, algebraic reasoning, and the ability to manipulate and solve systems of equations using various techniques such as substitution, elimination, or matrix methods.
-
mtschoon dernière édition par mtschoon

@Candace , bonjour,
Ici, la politesse n'est pas une option.
Merci de t'exprimer en français .
Traduction approximative :
Dans Math Olympiad, les problèmes impliquant des systèmes d'équations nécessitent souvent de résoudre plusieurs équations simultanément pour trouver les valeurs des variables. Ces problèmes testent les compétences en résolution de problèmes, le raisonnement algébrique et la capacité de manipuler et de résoudre des systèmes d'équations à l'aide de diverses techniques telles que la substitution, l'élimination ou les méthodes matricielles.
-
CCandace dernière édition par
-
mtschoon dernière édition par

Traduction : Hi =Salut
Bonjour @Candace