Equation différentielle non linéaire

Bonjour,
Y a-t-il parmis vous un balèze des equations différentielles ?
Je me casse la tête à résoudre cette équation différentielle non linéaire : 𝜭' = [2g(cos(𝜭)-cos(𝜭0)/l)^0.5
Je fais une étude sur la récupération d'energie dans une balancoire.
Toute aide rapide sera fortement appréciée.

@Léo-PIQUARD a dit dans Equation différentielle non linéaire :

Bonjour,
Y a-t-il parmis vous un balèze des equations différentielles ?
Je me casse la tête à résoudre cette équation différentielle non linéaire : 𝜭' = [2g(cos(𝜭)-cos(𝜭0)/l)^0.5
Je fais une étude sur la récupération d'energie dans une balancoire.
Toute aide rapide sera fortement appréciée.

Bonjour,

Je pense qu'on ne peut pas trouver de solution analytique, la résolution fait appel à une fonction spéciale (intégrale elliptique de Jacobi).

En général on fait plutôt ainsi :

Em = Ec + Ep
$Em=1/2∗mL2(dθdt)2+mgL(1−cos(θ))E_m = 1/2 * mL^2 (\frac{d\theta}{dt})^2 + mgL(1 - cos(\theta))$ (En prenant le niveau des Ep nulles au point bas du mouvement)

$dEmdt=0\frac{dE_m}{dt} = 0$ (L'énergie mécanique est conservative)

$12mL2∗2dθdt.d2θdt2+mgLsin(θ)dθdt=0\frac{1}{2}mL^2*2\frac{d\theta}{dt}.\frac{d^2\theta}{dt^2} + mgLsin(\theta)\frac{d\theta}{dt} = 0$

Et à vitesse non nulle cela se simplifie en :

$d2θdt2+gL.sin(θ)=0\frac{d^2\theta}{dt^2} + \frac{g}{L}.sin(\theta) = 0$
Equation classique du pendule simple.

De nouveau, cette équation ne se résout pas sans la fonction d'intégrale elliptique de Jacobi, MAIS ...

Pour des angles $θ\theta$ assez petits, on peut faire l'approximation $sin(θ)≃θsin(\theta) \simeq \theta$ (avec $θ\theta$ en radians), et si cette approximation est acceptable, il reste alors à résoudre l'équation : $d2θdt2+gL.θ=0\frac{d^2\theta}{dt^2} + \frac{g}{L}.\theta = 0$ ... qui ne présente pas de difficulté.

Bonjour Black-Jack,
Merci pour la rapidité de ta réponse.
Cette méthode marche pour des oscillation de faible amplitude, marche-t-elle aussi pour des amplitudes de 55° ?
Comme tu semble le sous-entendre, si tu as une piste qui n'est pas analytique, je suis preneur.

Bonjour,

On peut toujours faire une application par un tableur par de petits accroissements de temps, voila par exemple ce que cela peut donner.

Dans l'exemple :
Theta(0) = 55°,soit 0,95993109 rad (position angulaire initiale)
Theta'(0) = a rad/s (vitesse angulaire initiale)
L = 2m
g = 9,81 N/kg

La fonction traitée est $d2θdt2+gL.θ=0\frac{d^2\theta}{dt^2} + \frac{g}{L}.\theta = 0$

Voila une copie écran du début :

L'axe des abscisses est l'axe des temps gradué en s
L'axe des ordonnées est est l'angle theta (en radians)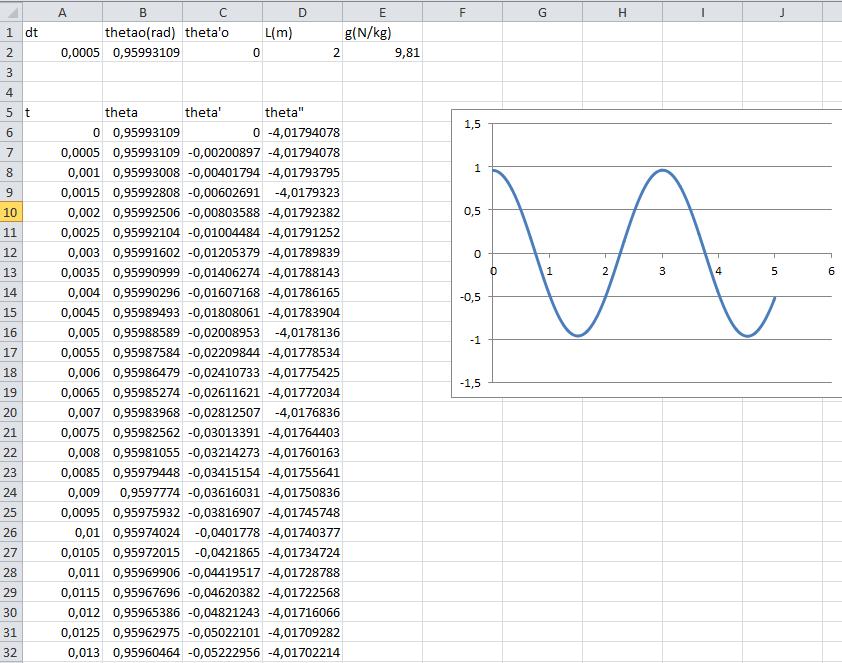

Sans titre.png

Tu peux faire l'exercice pour l'équation qui remplace sin(theta) par theta et en comparant les graphes; estimer l'erreur faite.

:

Rebonjour,

Voila ce que cela donne dans les mêmes conditions que ma réponse précédente mais en faisant l'approximation theta = sin(theta)

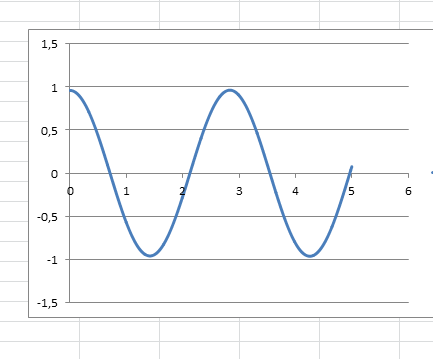
Sans titre.png

On voit la différence marquée (puisque l'angle n'est pas ici "petit"), mais reste à voir si c'est ou non acceptable dans l'optique de l'exercice.

Merci pour ces éléments très concrets et intéressants. Ca résout mon problème.