Suites de Syracuse : probabilités de décroissance

Bonjour
Je souhaiterais soumettre à vos avis un document PDF : comment le poster ?
Merci

@Azar Bonjour,

Pour information :
https://forum.mathforu.com/topic/1383/stop-lire-ce-sujet-tu-devras-avant-de-poster-ton-message.

Le scan ou un lien de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Écris l'énoncé, tes éléments de réponse et indique la question qui te pose problème. Tu obtiendras alors des pistes de résolution.

Bonjour,

Pour consultation éventuelle :
http://www.probleme-syracuse.fr/math.html

Bonjour, je ne suis pas mathématicien du tout, très novice donc, et je suis tombé sur cette conjoncture hier.

Par curiosité, j'ai essayé de trouver un modèle pour représenter cela. Sans aucune prétention, je voudrais savoir si mon raisonnement est juste, et si il démontre quoi que ce soit.

D'abord, d'un point de vue logique, tout nombre impair donnera un nombre pair une fois appliqué le X3+1. Et tout nombre pair sera divisé au moins une fois par deux ou plus.

Pour représenter cela, j'ai un paquet magique, ou dès lors qu'on tombe sur un nombre de ce paquet, on retombe sur 1 :

Paquet magique 1 : 2,4,8,16,32,64,128,256...

Tout nombre paire de ce paquet ira a 1. Sachant que tout nombre pair non dans ce paquet finira par donner un nombre impaire à sa dernière division par 2, avant donc d'être multiplié par 3+1.

Pour ceux là, pour chaque nombre impair, j'ai un paquet qui lui est lié , ses doubles, les doubles de ses doubles et ainsi de suite. Car un 3n+1 est toujours suivi d'un ou plusieurs divisé par 2, lui même suivi d'un 3n+1 amenant à un nouveau nombre impaire.

3 : 6, 12, 24, 48, 96...
5 : 10, 20, 40, 80...
7 : 14, 28, 56, 112...
9 : 18, 36, 72...
11: 22, 44, 88

Normalement, avec une telle répartition, je dispose de tous les nombres. Si je cherche 8, je vais dans le paquet 1, si je cherche 14, dans le paquet 7. Si je cherche 112, je vais toujours dans le paquet 7.

Le paquet 7 correspond à tous les nombre qui utiliseront directement la suite lié au numéro 7.

Pour connaître le lien entre les paquets, c'est à dire quand je suis arrivé à mon chiffre impair, dans quel groupe je vais une fois 3n+ a appliqué, on peut analyser tous les doubles pour lesquels, le double moins 1, est divisible par 3. On peut justifier cette approche du fait que chaque X3+1 est nécessairement suivi d'un divisé par 2. Donc un double moins 1 doit être divisible par trois.

Paquet 1: un chiffre sur deux en commençant par le secon est divisible par 3, soit :

1= (4 - 1) / 3,
5 = (16 - 1) / 3
21 = (64 - 1) / 3
...

Ce que cela signifie, c'est que si on donne un chiffre pair du paquet 5, ou 5, ou un nombre divisible par 3 une fois retranché 1 d'une des paire du paquet 5, on enchaînera nécessairement sur la suite 1.

Paquet 3 : aucun pair de ce paquet est divisible par 3, une fois retranché un. Ce qui signifie, qu'à part si on donne 3 au départ, ou un nombre pair de ce paquet, jamais on retrouvera 3 au milieu d'une séquence.

Paquet 5 : cette fois-ci un nombre sur 2 en commençant par le premier élément
3 = (10 - 1) / 3
13 = (40-1)/3
53 = (160-1)/3
...

Ce que cela signifie, c'est que si on donne 5, ou un double présent dans ce paquet, on aura la suite de 5 ( dont on a vu qu'elle contient la suite de 1). Sachant ici que lorsqu'on tombe sur 3, 13, 53 ..., on aura ensuite la séquence de 5.

La logique est la même pour les autres.

Paquet 7 :
9 : (28-1)/3
37 : (112-1)/3
...

Paquet 9 :
Aucun divisible par 3.

Paquet 11:
7 : (22-1)/3
29 : (88-1)/3
...

Paquet 13:
17 : (52-1) / 3
...
Paquet 15
Aucun divisible

Paquet 17
11 : (34-1)/3
...

J'arrête là, mais on peut voir que tous les chiffres impair sont présent jusqu'à jusqu'à 15 dans les liens.

Si on me donne 13, je vais naviguer dans les paquets de la sorte : 13 - 5 - 1

Si on me donne 11 : 11 - 17 - 13 - 5 - 1...

On constate d'ailleurs que lorsque deux séries sont liés, l'un aura vu ses doubles divisibles par 3 une fois retranché à partir de la première position et une fois sur deux, quand l'autre sera aussi une fois sur deux, mais en partant de la seconde position.

A priori, en distribuant les nombres de cette façon, nous n'avons pas de doublons, pas de séquence doublé et j'espère l'exhaustivité des nombres. Tous sont liés à un moment donné au paquet 1.

En espérant avoir été le plus clair possible.

Pour conclure,

La multiplication par n+3 d'un impair lui même issu d'un divisible par trois une fois retranché 1, permet la navigation dans les groupes, sans jamais retombé dans un groupe existant, à l'exception du groupe premier, pour qui 1 x 3 + 1 est toujours égale à sa double division.

Chaque double des paquets, une fois débarrassé de celui non divisible par 3, une fois retranché 1, voit une différence de 4 avec le paquet d'après. Bref je ne suis pas assez calé, loin de là, mais ça pourrait t'être également la clé de l'unicité des séquences, ou la variation amené par un n*3+1 d'un impaire lui même issu d'un divisible par 3 une fois retranché...

On voit aussi que que chaque nombre impaire contient la liste impaire du suivant (+n au fur et à mesure qu'on avance) ou du précédent (au fur et à mesure qu'on avance) une fois sur deux. Sauf pour les non divisibles par 3 ( leur double, pas eux même).

Donc 5 possède 3. (Où l'inverse selon la définition qu'on donne a possède)
7 possède 9
11 possède 7
13 possède 17
17 possède 11.

En espérant avoir été le plus clair possible. Je vois un modèle qui me paraît cohérent, et qui de façon logique explique ce qui se passe. Est-ce cohérent pour autant ? Est-ce juste une représentation, ou permet-elle au contraire de comprendre les mécanismes en place ?

Juste pour information sur la distribution

Paquet 1
1, 5, 21, 85, 341, 1365, 5461, 21845, 87381, 349525, 1398101, 5592405, 22369621, 89478485

Informatif (21 - 5)/1 = 16
(85-21)/1 = 64
(341 - 85)/1 = 256
Sans doute logique, et sans forcément que ça signifie quelque chose, mais on constate à chaque fois la puissance de 2 qui mène à 1.
=> 4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864,

Paquet 3

Paquet 5
3, 13, 53, 213, 853, 3413, 13653, 54613, 218453, 873813, 3495253, 13981013, 55924053, 223696213, 894784853
=> 2 [(13-3) / 2], 8, 32, 128, 512, 2048, 8192, 32768, 131072, 524288, 2097152, 8388608, 33554432, 134217728,
Paquet 7
9, 37, 149, 597, 2389, 9557, 38229, 152917, 611669, 2446677, 9786709, 39146837, 156587349, 626349397
=>4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864,
Paquet 9

Paquet 11
7, 29, 117, 469, 1877, 7509, 30037, 120149, 480597, 1922389, 7689557, 30758229, 123032917, 492131669, 1968526677
=>2, 8, 32, 128, 512, 2048, 8192, 32768, 131072, 524288, 2097152, 8388608, 33554432, 134217728,
Paquet 13
17, 69, 277, 1109, 4437, 17749, 70997, 283989, 1135957, 4543829, 18175317, 72701269, 290805077, 1163220309
=>4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864,
Paquet 15

Paquet 17
11, 45, 181, 725, 2901, 11605, 46421, 185685, 742741, 2970965, 11883861, 47535445, 190141781, 760567125, 3042268501

2, 8, 32, 128, 512, 2048, 8192, 32768, 131072, 524288, 2097152, 8388608, 33554432, 134217728,
Paquet 19
25, 101, 405, 1621, 6485, 25941, 103765, 415061, 1660245, 6640981, 26563925, 106255701, 425022805, 1700091221

4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864,
Paquet 21

Paquet 23
15, 61, 245, 981, 3925, 15701, 62805, 251221, 1004885, 4019541, 16078165, 64312661, 257250645, 1029002581, 4116010325

Paquet 25
33, 133, 533, 2133, 8533, 34133, 136533, 546133, 2184533, 8738133, 34952533, 139810133, 559240533, 2236962133

Paquet 27

Paquet 29
19, 77, 309, 1237, 4949, 19797, 79189, 316757, 1267029, 5068117, 20272469, 81089877, 324359509, 1297438037, 5189752149

Paquet 31
41, 165, 661, 2645, 10581, 42325, 169301, 677205, 2708821, 10835285, 43341141, 173364565, 693458261, 2773833045

Paquet 33

Paquet 35
23, 93, 373, 1493, 5973, 23893, 95573, 382293, 1529173, 6116693, 24466773, 97867093, 391468373, 1565873493, 6263493973

Paquet 37
49, 197, 789, 3157, 12629, 50517, 202069, 808277, 3233109, 12932437, 51729749, 206918997, 827675989, 3310703957

Paquet 39

Paquet 41
27, 109, 437, 1749, 6997, 27989, 111957, 447829, 1791317, 7165269, 28661077, 114644309, 458577237, 1834308949, 7337235797

Paquet 43
57, 229, 917, 3669, 14677, 58709, 234837, 939349, 3757397, 15029589, 60118357, 240473429, 961893717, 3847574869

Paquet 45

Paquet 47
31, 125, 501, 2005, 8021, 32085, 128341, 513365, 2053461, 8213845, 32855381, 131421525, 525686101, 2102744405, 8410977621

Paquet 49
65, 261, 1045, 4181, 16725, 66901, 267605, 1070421, 4281685, 17126741, 68506965, 274027861, 1096111445, 4384445781

Paquet 51

Paquet 53
35, 141, 565, 2261, 9045, 36181, 144725, 578901, 2315605, 9262421, 37049685, 148198741, 592794965, 2371179861, 9484719445

Paquet 55
73, 293, 1173, 4693, 18773, 75093, 300373, 1201493, 4805973, 19223893, 76895573, 307582293, 1230329173, 4921316693

Paquet 57

Paquet 59
39, 157, 629, 2517, 10069, 40277, 161109, 644437, 2577749, 10310997, 41243989, 164975957, 659903829, 2639615317, 10558461269

Paquet 61
81, 325, 1301, 5205, 20821, 83285, 333141, 1332565, 5330261, 21321045, 85284181, 341136725, 1364546901, 5458187605

Paquet 63

Paquet 65
43, 173, 693, 2773, 11093, 44373, 177493, 709973, 2839893, 11359573, 45438293, 181753173, 727012693, 2908050773, 11632203093

Paquet 67
89, 357, 1429, 5717, 22869, 91477, 365909, 1463637, 5854549, 23418197, 93672789, 374691157, 1498764629, 5995058517

Paquet 69

Paquet 71
47, 189, 757, 3029, 12117, 48469, 193877, 775509, 3102037, 12408149, 49632597, 198530389, 794121557, 3176486229, 12705944917

Paquet 73
97, 389, 1557, 6229, 24917, 99669, 398677, 1594709, 6378837, 25515349, 102061397, 408245589, 1632982357, 6531929429

Paquet 75

Paquet 77
51, 205, 821, 3285, 13141, 52565, 210261, 841045, 3364181, 13456725, 53826901, 215307605, 861230421, 3444921685, 13779686741

Paquet 79
105, 421, 1685, 6741, 26965, 107861, 431445, 1725781, 6903125, 27612501, 110450005, 441800021, 1767200085, 7068800341

Paquet 81

Paquet 83
55, 221, 885, 3541, 14165, 56661, 226645, 906581, 3626325, 14505301, 58021205, 232084821, 928339285, 3713357141, 14853428565

Paquet 85
113, 453, 1813, 7253, 29013, 116053, 464213, 1856853, 7427413, 29709653, 118838613, 475354453, 1901417813, 7605671253

Paquet 87

Paquet 89
59, 237, 949, 3797, 15189, 60757, 243029, 972117, 3888469, 15553877, 62215509, 248862037, 995448149, 3981792597, 15927170389

Paquet 91
121, 485, 1941, 7765, 31061, 124245, 496981, 1987925, 7951701, 31806805, 127227221, 508908885, 2035635541, 8142542165

Paquet 93

Paquet 95
63, 253, 1013, 4053, 16213, 64853, 259413, 1037653, 4150613, 16602453, 66409813, 265639253, 1062557013, 4250228053, 17000912213

Paquet 97
129, 517, 2069, 8277, 33109, 132437, 529749, 2118997, 8475989, 33903957, 135615829, 542463317, 2169853269, 8679413077

Paquet 99

Paquet 101
67, 269, 1077, 4309, 17237, 68949, 275797, 1103189, 4412757, 17651029, 70604117, 282416469, 1129665877, 4518663509, 18074654037

Paquet 103
137, 549, 2197, 8789, 35157, 140629, 562517, 2250069, 9000277, 36001109, 144004437, 576017749, 2304070997, 9216283989

Paquet 105

Paquet 107
71, 285, 1141, 4565, 18261, 73045, 292181, 1168725, 4674901, 18699605, 74798421, 299193685, 1196774741, 4787098965, 19148395861

Paquet 109
145, 581, 2325, 9301, 37205, 148821, 595285, 2381141, 9524565, 38098261, 152393045, 609572181, 2438288725, 9753154901

Paquet 111

Paquet 113
75, 301, 1205, 4821, 19285, 77141, 308565, 1234261, 4937045, 19748181, 78992725, 315970901, 1263883605, 5055534421, 20222137685

Paquet 115
153, 613, 2453, 9813, 39253, 157013, 628053, 2512213, 10048853, 40195413, 160781653, 643126613, 2572506453, 10290025813

Paquet 117

Paquet 119
79, 317, 1269, 5077, 20309, 81237, 324949, 1299797, 5199189, 20796757, 83187029, 332748117, 1330992469, 5323969877, 21295879509

Paquet 121
161, 645, 2581, 10325, 41301, 165205, 660821, 2643285, 10573141, 42292565, 169170261, 676681045, 2706724181, 10826896725

Paquet 123

Paquet 125
83, 333, 1333, 5333, 21333, 85333, 341333, 1365333, 5461333, 21845333, 87381333, 349525333, 1398101333, 5592405333, 22369621333

Paquet 127
169, 677, 2709, 10837, 43349, 173397, 693589, 2774357, 11097429, 44389717, 177558869, 710235477, 2840941909, 11363767637

Paquet 129

Paquet 131
87, 349, 1397, 5589, 22357, 89429, 357717, 1430869, 5723477, 22893909, 91575637, 366302549, 1465210197, 5860840789, 23443363157

Paquet 133
177, 709, 2837, 11349, 45397, 181589, 726357, 2905429, 11621717, 46486869, 185947477, 743789909, 2975159637, 11900638549

Paquet 135

Paquet 137
91, 365, 1461, 5845, 23381, 93525, 374101, 1496405, 5985621, 23942485, 95769941, 383079765, 1532319061, 6129276245, 24517104981

Paquet 139
185, 741, 2965, 11861, 47445, 189781, 759125, 3036501, 12146005, 48584021, 194336085, 777344341, 3109377365, 12437509461

Paquet 141

Paquet 143
95, 381, 1525, 6101, 24405, 97621, 390485, 1561941, 6247765, 24991061, 99964245, 399856981, 1599427925, 6397711701, 25590846805

Paquet 145
193, 773, 3093, 12373, 49493, 197973, 791893, 3167573, 12670293, 50681173, 202724693, 810898773, 3243595093, 12974380373

Paquet 147

Paquet 149
99, 397, 1589, 6357, 25429, 101717, 406869, 1627477, 6509909, 26039637, 104158549, 416634197, 1666536789, 6666147157, 26664588629

Paquet 151
201, 805, 3221, 12885, 51541, 206165, 824661, 3298645, 13194581, 52778325, 211113301, 844453205, 3377812821, 13511251285

Paquet 153

Paquet 155
103, 413, 1653, 6613, 26453, 105813, 423253, 1693013, 6772053, 27088213, 108352853, 433411413, 1733645653, 6934582613, 27738330453

Paquet 157
209, 837, 3349, 13397, 53589, 214357, 857429, 3429717, 13718869, 54875477, 219501909, 878007637, 3512030549, 14048122197

Paquet 159

Paquet 161
107, 429, 1717, 6869, 27477, 109909, 439637, 1758549, 7034197, 28136789, 112547157, 450188629, 1800754517, 7203018069, 28812072277

Paquet 163
217, 869, 3477, 13909, 55637, 222549, 890197, 3560789, 14243157, 56972629, 227890517, 911562069, 3646248277, 14584993109

Paquet 165

Paquet 167
111, 445, 1781, 7125, 28501, 114005, 456021, 1824085, 7296341, 29185365, 116741461, 466965845, 1867863381, 7471453525, 29885814101

Paquet 169
225, 901, 3605, 14421, 57685, 230741, 922965, 3691861, 14767445, 59069781, 236279125, 945116501, 3780466005, 15121864021

Paquet 171

Paquet 173
115, 461, 1845, 7381, 29525, 118101, 472405, 1889621, 7558485, 30233941, 120935765, 483743061, 1934972245, 7739888981, 30959555925

Paquet 175
233, 933, 3733, 14933, 59733, 238933, 955733, 3822933, 15291733, 61166933, 244667733, 978670933, 3914683733, 15658734933

Paquet 177

Paquet 179
119, 477, 1909, 7637, 30549, 122197, 488789, 1955157, 7820629, 31282517, 125130069, 500520277, 2002081109, 8008324437, 32033297749

Paquet 181
241, 965, 3861, 15445, 61781, 247125, 988501, 3954005, 15816021, 63264085, 253056341, 1012225365, 4048901461, 16195605845

Paquet 183

Paquet 185
123, 493, 1973, 7893, 31573, 126293, 505173, 2020693, 8082773, 32331093, 129324373, 517297493, 2069189973, 8276759893, 33107039573

Paquet 187
249, 997, 3989, 15957, 63829, 255317, 1021269, 4085077, 16340309, 65361237, 261444949, 1045779797, 4183119189, 16732476757

Paquet 189

Paquet 191
127, 509, 2037, 8149, 32597, 130389, 521557, 2086229, 8344917, 33379669, 133518677, 534074709, 2136298837, 8545195349, 34180781397

Paquet 193
257, 1029, 4117, 16469, 65877, 263509, 1054037, 4216149, 16864597, 67458389, 269833557, 1079334229, 4317336917, 17269347669

Paquet 195

Paquet 197
131, 525, 2101, 8405, 33621, 134485, 537941, 2151765, 8607061, 34428245, 137712981, 550851925, 2203407701, 8813630805, 35254523221

Paquet 199
265, 1061, 4245, 16981, 67925, 271701, 1086805, 4347221, 17388885, 69555541, 278222165, 1112888661, 4451554645, 17806218581

Paquet 201

Paquet 203
135, 541, 2165, 8661, 34645, 138581, 554325, 2217301, 8869205, 35476821, 141907285, 567629141, 2270516565, 9082066261, 36328265045

Paquet 205
273, 1093, 4373, 17493, 69973, 279893, 1119573, 4478293, 17913173, 71652693, 286610773, 1146443093, 4585772373, 18343089493

Paquet 207

Paquet 209
139, 557, 2229, 8917, 35669, 142677, 570709, 2282837, 9131349, 36525397, 146101589, 584406357, 2337625429, 9350501717, 37402006869

Paquet 211
281, 1125, 4501, 18005, 72021, 288085, 1152341, 4609365, 18437461, 73749845, 294999381, 1179997525, 4719990101, 18879960405

Paquet 213

Paquet 215
143, 573, 2293, 9173, 36693, 146773, 587093, 2348373, 9393493, 37573973, 150295893, 601183573, 2404734293, 9618937173, 38475748693

Paquet 217
289, 1157, 4629, 18517, 74069, 296277, 1185109, 4740437, 18961749, 75846997, 303387989, 1213551957, 4854207829, 19416831317

Paquet 219

Paquet 221
147, 589, 2357, 9429, 37717, 150869, 603477, 2413909, 9655637, 38622549, 154490197, 617960789, 2471843157, 9887372629, 39549490517

Paquet 223
297, 1189, 4757, 19029, 76117, 304469, 1217877, 4871509, 19486037, 77944149, 311776597, 1247106389, 4988425557, 19953702229

Paquet 225

Paquet 227
151, 605, 2421, 9685, 38741, 154965, 619861, 2479445, 9917781, 39671125, 158684501, 634738005, 2538952021, 10155808085, 40623232341

Paquet 229
305, 1221, 4885, 19541, 78165, 312661, 1250645, 5002581, 20010325, 80041301, 320165205, 1280660821, 5122643285, 20490573141

Paquet 231

Paquet 233
155, 621, 2485, 9941, 39765, 159061, 636245, 2544981, 10179925, 40719701, 162878805, 651515221, 2606060885, 10424243541, 41696974165

Paquet 235
313, 1253, 5013, 20053, 80213, 320853, 1283413, 5133653, 20534613, 82138453, 328553813, 1314215253, 5256861013, 21027444053

Paquet 237

Paquet 239
159, 637, 2549, 10197, 40789, 163157, 652629, 2610517, 10442069, 41768277, 167073109, 668292437, 2673169749, 10692678997, 42770715989

Paquet 241
321, 1285, 5141, 20565, 82261, 329045, 1316181, 5264725, 21058901, 84235605, 336942421, 1347769685, 5391078741, 21564314965

Paquet 243

Paquet 245
163, 653, 2613, 10453, 41813, 167253, 669013, 2676053, 10704213, 42816853, 171267413, 685069653, 2740278613, 10961114453, 43844457813

Paquet 247
329, 1317, 5269, 21077, 84309, 337237, 1348949, 5395797, 21583189, 86332757, 345331029, 1381324117, 5525296469, 22101185877

Paquet 249

Paquet 251
167, 669, 2677, 10709, 42837, 171349, 685397, 2741589, 10966357, 43865429, 175461717, 701846869, 2807387477, 11229549909, 44918199637

Paquet 253
337, 1349, 5397, 21589, 86357, 345429, 1381717, 5526869, 22107477, 88429909, 353719637, 1414878549, 5659514197, 22638056789

Paquet 255

Paquet 257
171, 685, 2741, 10965, 43861, 175445, 701781, 2807125, 11228501, 44914005, 179656021, 718624085, 2874496341, 11497985365, 45991941461

Paquet 259
345, 1381, 5525, 22101, 88405, 353621, 1414485, 5657941, 22631765, 90527061, 362108245, 1448432981, 5793731925, 23174927701

Paquet 261

Paquet 263
175, 701, 2805, 11221, 44885, 179541, 718165, 2872661, 11490645, 45962581, 183850325, 735401301, 2941605205, 11766420821, 47065683285

Paquet 265
353, 1413, 5653, 22613, 90453, 361813, 1447253, 5789013, 23156053, 92624213, 370496853, 1481987413, 5927949653, 23711798613

Paquet 267

Paquet 269
179, 717, 2869, 11477, 45909, 183637, 734549, 2938197, 11752789, 47011157, 188044629, 752178517, 3008714069, 12034856277, 48139425109

Paquet 271
361, 1445, 5781, 23125, 92501, 370005, 1480021, 5920085, 23680341, 94721365, 378885461, 1515541845, 6062167381, 24248669525

Paquet 273

Paquet 275
183, 733, 2933, 11733, 46933, 187733, 750933, 3003733, 12014933, 48059733, 192238933, 768955733, 3075822933, 12303291733, 49213166933

Paquet 277
369, 1477, 5909, 23637, 94549, 378197, 1512789, 6051157, 24204629, 96818517, 387274069, 1549096277, 6196385109, 24785540437

Paquet 279

Paquet 281
187, 749, 2997, 11989, 47957, 191829, 767317, 3069269, 12277077, 49108309, 196433237, 785732949, 3142931797, 12571727189, 50286908757

Paquet 283
377, 1509, 6037, 24149, 96597, 386389, 1545557, 6182229, 24728917, 98915669, 395662677, 1582650709, 6330602837, 25322411349

Paquet 285

Suite remarque sur la distribution des paquets
Un paquet sur 2 va prendre un paquet impair inférieur à lui-même.
Puis il va prendre tous les paquets supérieurs à lui, sachant que la (différence entre deux impairs) / par lui-même correspond à une partie de la suite magique du paquet 1.
L'autre paquet sur 2 prendra que des supérieurs, suivant la même logique, mais avec l'autre bout de la suite.

Exemple du paquet 1 : 5, 21 ,85 ...
(5-1) /1 = 4
(21-5) / 1 = 16
(85-21) /1 = 64

On a en gros deux suites possibles :

4, 16, 64, 256, 1024, 4096, 16384, 65536, 262144, 1048576, 4194304, 16777216, 67108864 (celle-là ira prendre que des impairs supérieurs)
2, 8, 32, 128, 512, 2048, 8192, 32768, 131072, 524288, 2097152, 8388608, 33554432, 134217728, (celle-là prendra un impair inférieur, puis que des pairs supérieur)

La fusion des deux suites correspond au paquet 1.

Si on pouvait montrer mathématiquement cette distribution, ne prouverait-on pas qu'on a l'intégralité des nombres (un impaire sur deux prend un inférieur à lui même, lui-même n'étant pas lien de lui-même, sauf pour le paquet 1, autosuffisant), qu'ils sont tous liés une seul fois ... ?

Le même arbre des paquets, dans l'ordre de passage (je ne met pas trop long, car ça devient illisible sinon => faudrait une option cache/affiche):

Etoile veut dire multiple de 3
Paquet 1 :
Propriétaire des impairs suivants 1 , 5 , 21 *, 85 , 341 , 1365 *, 5461 , 21845
Liste des doubles du paquet : 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096
(Différence entre deux double) / 1 :4, 16, 64, 256, 1024, 4096, 16384

Paquet 5 :
Propriétaire des impairs suivants 3 *, 13 , 53 , 213 *, 853 , 3413 , 13653 *, 54613 , 218453
Liste des doubles du paquet : 10, 20, 40, 80, 160, 320, 640, 1280, 2560, 5120, 10240, 20480
(Différence entre deux double) / 5 :2, 8, 32, 128, 512, 2048, 8192, 32768

Paquet 11 :
Propriétaire des impairs suivants 7 , 29 , 117 *, 469 , 1877 , 7509 *, 30037 , 120149 , 480597 *
Liste des doubles du paquet : 22, 44, 88, 176, 352, 704, 1408, 2816, 5632, 11264, 22528, 45056
(Différence entre deux double) / 11 :2, 8, 32, 128, 512, 2048, 8192, 32768

Paquet 7 :
Propriétaire des impairs suivants 9 *, 37 , 149 , 597 *, 2389 , 9557 , 38229 *, 152917
Liste des doubles du paquet : 14, 28, 56, 112, 224, 448, 896, 1792, 3584, 7168, 14336, 28672
(Différence entre deux double) / 7 :4, 16, 64, 256, 1024, 4096, 16384

Paquet 17 :
Propriétaire des impairs suivants 11 , 45 *, 181 , 725 , 2901 *, 11605 , 46421 , 185685 *, 742741
Liste des doubles du paquet : 34, 68, 136, 272, 544, 1088, 2176, 4352, 8704, 17408, 34816, 69632
(Différence entre deux double) / 17 :2, 8, 32, 128, 512, 2048, 8192, 32768

Paquet 23 :
Propriétaire des impairs suivants 15 *, 61 , 245 , 981 *, 3925 , 15701 , 62805 *, 251221 , 1004885
Liste des doubles du paquet : 46, 92, 184, 368, 736, 1472, 2944, 5888, 11776, 23552, 47104, 94208
(Différence entre deux double) / 23 :2, 8, 32, 128, 512, 2048, 8192, 32768

Paquet 13 :
Propriétaire des impairs suivants 17 , 69 *, 277 , 1109 , 4437 *, 17749 , 70997 , 283989 *
Liste des doubles du paquet : 26, 52, 104, 208, 416, 832, 1664, 3328, 6656, 13312, 26624, 53248
(Différence entre deux double) / 13 :4, 16, 64, 256, 1024, 4096, 16384

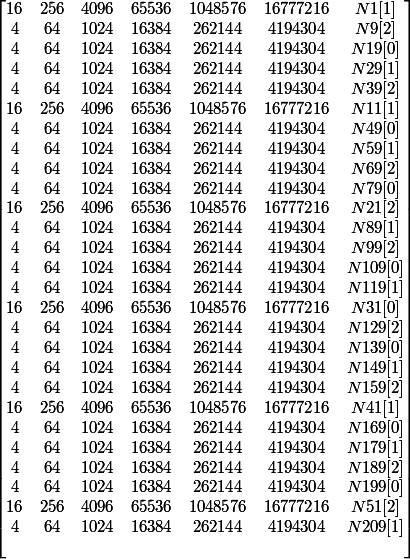
Pour info, voici la liste distribuée de ces paquets, mais ordonné par leur premier impair.

Avec leur double correspondant (on fait 3xn+1)!

(Différence entre deux double) / nombre de référence (paquet)

Il faut aussi faire la Syracuse de 5n +1.

Si j'ai bien fait mon truc, celle-ci se vérifie que pour certains entiers se terminant par 1 ou par 9. Enfin, tous les entiers se terminant par 1 ou par 9, de bout en bout de la chaîne.

Si on prend en entré 171127603 (avant dernière ligne, propriété de 51, lui-même propriété de 1), on va bien retrouvé notre suite. Si mon truc est exhaustif, certains entiers terminant par 1 ou par 9, suivent une "conjoncture" de 5n+1.

Le tableau des suites de doubles :

Le tableau des différences divisé par le propriétaire: