problème probabilité
-
Maxime 174 dernière édition par Maxime 174
bonsoir j'ai un exercice de probabilité et je n'arrive pas à résoudre la dernière question.
un CSM a deux classes de terminales D. La TD1 et la TD2. c'est deux classes contiennent respectivement 60% et 44% de filles
la TD1 a deux plus d'élèves que la TD2
on désigne D1 , D2 et F les évènements suivants :
D1:<<l'élève choisi est en TD1>>
D2:<<l'élève choisi est en TD2>>
F:<<l'élève choisi est une fille>>-
a) démontrer que la probabilité de D1 est 2/3
b) quelle est la probabilité de D2 -
a) calculé P(D1 intert F)
b) calculé la probabilité de F -
sachant que l'élève choisi est une fille, quelle est la probabilité que cette fille soit en TD1
-
on suppose que la TD1 contient 30 filles déterminer l'effectif de chacune des deux classes.
réponse
tout d'abord j'ai fait un arbre pondéré traduisant la situation. -
a) on a P(D1)=2/5x+3/5x=2(1-x) après calcul on trouve x=2/3 d'où P(D1)=2/3
b ) d'où P(B)=1/3 -
a) P(D1 intert F) =3/5×2/3=2/5
b) P(F) = 2/3×3/5+1/3×11/25=41/75
P(D1) sachant F=0,4/0,54=0,74
c'est au niveau de la dernière question que je bloque toujours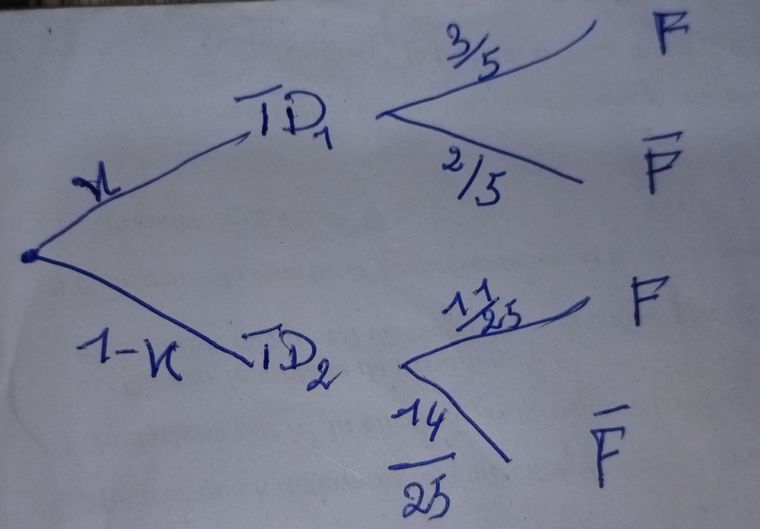
-
-
HHenri dernière édition par
Soit nnn le nombre d'élèves de la TD2. Alors, par hypothèse, celui de la TD1 est 2n2n2n. D'où P(D1)=2n3n=23P(D1)=\frac{2n}{3n}=\frac23P(D1)=3n2n=32.
4. Si la TD1 a 303030 filles, elle a 202020 garçons, soit 505050 élèves. Et la TD2 en a 252525.
-
BBlack-Jack dernière édition par
Bonjour,
Alternative pour le calculs des effectifs ... sans aucun calcul de probabilité (donc ce n'est pas ce qui est attendu, mais uniquement pour montrer une autre approche) :
On traduit mathématiquement les propositions :
F1 = 0,6.(F1+G1)
F2 = 0,44.(F2+G2)
F1+G1 = 2.(F2+G2)
F1 = 30Système simple qui permet de calculer directement :
F1 = 30
G1 = 20
F2 = 11
G2 = 14Soit 50 élèves en TD1 et 25 en TD2.
-
Maxime 174 dernière édition par
@Black-Jack bonjour
je comprends mieux maintenant merci beaucoup pour votre aide