Exercice statistique - L2

Bonjour à tous !
Je dois résoudre un exercice statistique sur un test pour détecter une maladie.
En gros il y a deux groupes, un avec 50 malades et un autre avec 50 personnes saines; et on fait passer le test aux deux groupes.
Ce test consiste à injecter un produit à une personne qui va développer une réaction immunitaire de la peau donc un bouton. On mesure la taille du bouton pour mesurer cette réponse immunitaire; donc en théorie plus le bouton est grand, plus il y a eu de réponse immunitaire, plus la personne est malade.
La réaction immunitaire suit une loi normale dans chaque cas

Entre 2 et 4mm la réaction est douteuse
Entre 4 et 15mm la réaction est faible à forte donc le test est positif.

On a les résultats intermédiaires suivants: (Rc1) = groupe malade (Rc2) = groupe sain

(Rc1) = 761.0 mm
Σ(Rc1²) = 11634.1 mm²

Σ(Rc2) = 203.1 mm
Σ(Rc2² ) = 862.3 mm²

Je dois calculer la moyenne, la variance et l'écart-type pour les deux groupes, mais je ne vois pas bien comment faire (au vu de mon très faible niveau en maths :gene: )

Pour le premier groupe, pour faire la moyenne, j'ai divisé 761.0 par 50.
Pour le reste je ne comprend juste pas ce que signifie le Σ dans Σ(Rc2² ) et Σ(Rc1² )

Merci pour votre aide !

@Salome-b Bonsoir,

Le signe $∑\displaystyle\sum$ est le signe somme ;
Tu dois avoir dans le cours les relations pour calculer la moyenne, la variance et l'écart-type.

Ok donc en fait pour Σ(Rc1² ) par exemple, on a pris chaque terme qu'on a élevé au carré et qu'on a additionné ?
Pour le cours j'ai la formule classique pour calculer la variance d'un échantillon, mais comment on fait quand on a pas tous les termes de la série de valeur mais juste leur somme comme ici, pour trouver les écarts à la moyenne à utiliser dans la formule ?

Merci

@Salome-b

Tu as quelle formule pour la variance ?

Tu dois utiliser : $\dfrac{1}{n}\displaystyle\sum n_ix_i^2- (\overline x)^2$

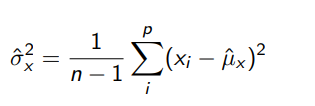
J'ai cette formule pour calculer la variance d'un échantillon

J'ai aussi le développement de koenig !

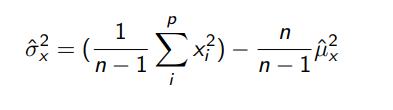
Je pense que je peux utiliser ça !?

@Salome-b

Oui, c'est cette formule qu'il faut utiliser.

Ok merci
Donc pour la variance du groupe 1 j'ai trouvé 4,82 en mettant à la place de Σxi² 760² et à la place de mu²x la moyenne que j'ai calculé donc 4,062.
Ca paraît cohérant ?

@Salome-b

Attention $R c 1$ correspond à $x_i$ .

Ce message a été supprimé !

@Noemi D'accord donc je dois utiliser (Rc1²) donc 11634,1 ?

@Salome-b

Oui.

ok merci pour votre aide !