convergence de suite

Coucou
j'ai une question qui me pose problème! c'est sur les suites!
Il s'agit de montrer que la suite est convergente. Je viens de montrer qu'elle avait une limite finie (par le theo des gendarmes) Il me reste à montrer qu'elle est est monotone et la je bloque. Car la suite est définie par un encadrement.
j'ai essayé par récurrence bof, Un+1 - Un rebof , etude de fonctions peut être?
Voila la suite
1 + (1/4)^n <= Un <= 2-n/(n+1).
merci pour votre aide

Ce message a été supprimé !

j'ai procédé en 2 étapes: d'abord sur la partie gauche de l'inégalité
Un>= 1+(1/4)^n
Un+1 >=1+(1/4)^(n+1)
Un+1 -Un >= -3/4*(1/4)^n <0 mais je suis pas certaine de pouvoir écrire cette inégalité...
Un+1<=Un
Puis la partie droite
Un<= 2 - (n)/(n+1)
Un+1 <=2-(n+1)/(n+2)
Un+1 - Un <= -(n+1)/(n+2) + n/(n+1) = -1/((n+1)*(n+2)) <0
Un+1< = Un
Finalement pour tout n Un+1 <= Un donc (un) décroissante

Qu'en pensez vous?

@Black-Jack merci pour votre réponse mais je n'ai pas encore vu la fonction ln ni g''

@Logena a dit dans convergence de suite :

j'ai procédé en 2 étapes: d'abord sur la partie gauche de l'inégalité
Un>= 1+(1/4)^n
Un+1 >=1+(1/4)^(n+1)
Un+1 -Un >= -3/4*(1/4)^n <0 mais je suis pas certaine de pouvoir écrire cette inégalité...
Un+1<=Un
Puis la partie droite
Un<= 2 - (n)/(n+1)
Un+1 <=2-(n+1)/(n+2)
Un+1 - Un <= -(n+1)/(n+2) + n/(n+1) = -1/((n+1)*(n+2)) <0
Un+1< = Un
Finalement pour tout n Un+1 <= Un donc (un) décroissante

Qu'en pensez vous?

Bonjour,

Non, tu ne peux pas faire cela.

Par exemple, tu écris :

Un>= 1+(1/4)^n
U(n+1) >=1+(1/4)^(n+1)
U(n+1) -Un >= -3/4*(1/4)^n <0

Exemple, avec n = 1, cela donnerait :

U1>= 5/4
U2 >=17/16

Sans rien d'autre comme justification, ou pourrait par exemple avoir :
U1 = 3 (qui est bien vérifié par U1 >= 5/4)
et
U2 = 5 (qui est bien vérifié par U2 >= 17/16)

Tu ne peux donc pas en déduire que U(n+1) <= U(n)

Pareil pour la "partie droite", ce que tu as écrit n'est pas correct.

J'ai supprimé ma première intervention où, il y avait des erreurs.

Bonjour,

Je soupçonne une erreur dans ton énoncé.

Tu as écrit : 1 + (1/4)^n <= Un <= 2-n/(n+1).

As-tu essayé d'écrire : $(\frac{1}{4})^n \leq U_n \leq 2 - \frac{n}{n+1}$

ou bien : $(\frac{1}{4})^n \leq U_n \leq \frac{2-n}{n+1}$

Il faut montrer que les deux suites qui encadrent Un tendent vers 1 lorsque n tend vers l'infini.

On remarque que :
$1+(14)n1+(\frac{1}{4})^n$ = $1+1n4n1+\frac{1^n}{4^n}$
et
$2−nn+12-\frac{n}{n+1}$ = $1+n+1n+1−nn+11+\frac{n+1}{n+1}-\frac{n}{n+1}$

Les limites sont ensuite faciles à calculer.

@DenisDenis a dit dans convergence de suite :

Il faut montrer que les deux suites qui encadrent Un tendent vers 1 lorsque n tend vers l'infini.

On remarque que :
$1+(14)n1+(\frac{1}{4})^n$ = $1+1n4n1+\frac{1^n}{4^n}$
et
$2−nn+12-\frac{n}{n+1}$ = $1+n+1n+1−nn+11+\frac{n+1}{n+1}-\frac{n}{n+1}$

Les limites sont ensuite faciles à calculer.

Bonjour,

Je ne suis pas d'accord.

On doit montrer que la suite est monotone.
Ce que tu montres est que la suite converge (peut-être) vers 1, mais pas qu'elle converge d'une manière monotone.

Je soupçonne fort que (erreur très fréquente depuis qu'on enseigne plus correctement les priorités des opérations mathématiques)
le relation qu'a essayé d'écrire est la seconde de mon message précédent (même si ce n'est pas ce qu'il a réellement écrit).

Si oui, alors :

S'il s'agit de : 1 + (1/4)^n <= U(n) <= (2-n)/(n+1)

Il suffit de montrer que pour tout n de N, on a : "le minimum possible de U(n) est > que le maximum possible de U(n+1)"
soit donc que 1 + (1/4)^n > (2-(n+1))/((n+1)+1)

Soit f(n) = 1 + (1/4)^n - (2-(n+1))/((n+1)+1)
f(n) = 1 + (1/4)^n - (1-n)/(n+2)
f(n) = (1/4)^n + (2n+1)/(n+2)
f(n) > 0 pour tout n de N (comme somme de 2 quantités positives)

Donc, pout tout n de N, on a : 1 + (1/4)^n - (2-(n+1))/((n+1)+1)
1 + (1/4)^n > (2-(n+1))/((n+1)+1)

Donc pour tout n de N, le minimum possible de U(n) est > que le maximum possible de U(n+1)
--> La suite Un est donc strictement décroissante (donc monotone)

Si la relation de départ est vraiment la 1ère de mon message précédent, on peut procéder de manière équivalente à ce que j'ai fait ci-dessus ... mais l'étude du signe de

U(n) min - U(n+1) max est plus compliqué.

@Black-Jack a dit dans convergence de suite :

On doit montrer que la suite est monotone.

Les données du problème ne permettent pas de montrer que la suite est monotone. Soit par exemple la suite suivante :

Si n est pair Un = 1 + (1/4)^n
Si n est impair Un = 2-n/(n+1)

On a bien 1 + (1/4)^n <= Un <= 2-n/(n+1), mais la suite n'est pas monotone.
Soit il manque une donnée du problème, soit la propriété "monotone" n'est pas à démontrer.

@Logena a dit dans convergence de suite :

Il s'agit de montrer que la suite est convergente.

@Black-Jack a dit dans convergence de suite :

Bonjour,

Je soupçonne une erreur dans ton énoncé.

Tu as écrit : 1 + (1/4)^n <= Un <= 2-n/(n+1).

As-tu essayé d'écrire : $(\frac{1}{4})^n \leq U_n \leq 2 - \frac{n}{n+1}$

ou bien : $(\frac{1}{4})^n \leq U_n \leq \frac{2-n}{n+1}$

Certainement pas.
$2−nn+1\frac{2-n}{n+1}$ va être négatif pour tout n supérieur à 2, alors que $(\frac{1}{4})^n$ est toujours positif.

Il y a une bisbrouille dans l'énoncé.

Avec l'énoncé initial, on a ceci :

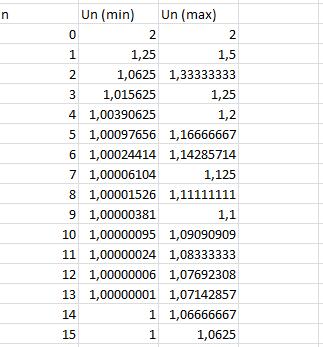
Sans titre.png

Ce qui ne peut pas permettre, en effet, de dire si la suite est ou non monotone.

On aurait pu, si Un(min) > U(n+1) max pour tout n de N
ou bien si Un(max) < U(n+1) min pour tout n de N
... mais ce n'est pas le cas.

Sauf nouvelle distraction.

Bonjour à tous et bonne semaine.

J'ai des activités « prioritaires » qui m'occupent beaucoup et expliquent ma "non-présence" sur le forum.
Je l’ai indiqué à Casebas, bien sûr.
Je ne fais que passer….

Bonjour @Logena
Seulement une réflexion car @DenisDenis t’a donné la marche à suivre.
Tu aurais dû éviter de parler de monotonie (qui n’a rien à voir dans cet exercice) car cela a crée des complications dans ton topic.

Tu as dû mal interpréter deux propriétés usuelles de ton cours (toute suite croissante et majorée est convergente et toute suite décroissante et minorée est convergente).
Cela ne veut pas dire que toute suite convergente doit être forcément monotone !...
Une suite ni croissante, ni décroissante peut être convergente.

Je te rappelle le théorème dit des « deux gendarmes » qui doit être démontré dans ton cours :

Hypothèse : A partir d'un certain rang, $Vn≤Un≤WnV_n\le U_n\le W_n$

Si les suites $V_n)$ et $W_n)$ convergent vers une même limite L, alors la suite $U_n)$ converge vers cette même limite L
Ici, L=1.
C'est tout .

Reposte si tu as des difficultés à trouver les limites de $V_n)$ et $W_n)$
avec $Vn=1+(14)nV_n=1+\biggr(\dfrac{1}{4}\biggr)^n$ et $Wn=2−nn+1W_n=2-\dfrac{n}{n+1}$

Pour consultation, tu peux regarder cette vidéo qui traite la limite d'une fonction avec ce théorème des deux gendarmes.
https://www.youtube.com/watch?v=Eo1jvPphja0

Bonne lecture éventuelle.