résoudre une équation avec des valeurs absolues

[Hakim93]

comment résoudre : abs(x) + abs (x-2) = abs(x+5)

[mtschoon]

@Hakim93 , bonjour,

Ici, la politesse n'est pas une option.
Il faudra y penser une autre fois.

Rappel :
Tu dois savoir que :
Pour $a>0$ : |a|=a
Pour $a=0$ : |a|=0
Pour $a<0$ : |a|=-a

Pistes,

Soit (E) l'équation : $|x|+|x-2|=|x+5|$

Je te conseille de disposer ton travail sous forme d'un tableau

je t'en joins un qu'il faut compléter :

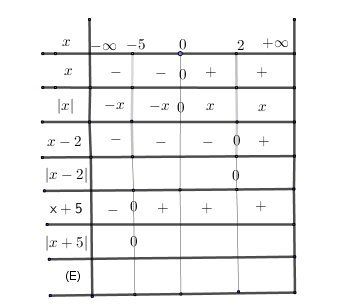
Je te traite le cas de la première colonne : $x\in ]-\infty ,-5[$ :

(E) s'écrit : $-x+(-x+2)=-x-5$ <=>$x=7$
Impossible car $7$ n'appartient pas à $x\in ]-\infty ,-5[$

Tu continues.

Reposte si besoin.

[Black-Jack]

Bonjour,

Il y a 3 valeurs de x, soit 0, 2 et -5 qui influence.

On va donc "diviser les x" en 4 intervalles.

a) x compris dans ]-oo ; -5]
b) x compris dans [-5 ; 0]
c) x compris dans ]0 ; 2[
d) x compris dans [2 ; +oo[

1°) Pour x compris dans ]-oo ; -5], on a :
abs(x) = -x
abs(x-2) = 2-x
abs(x+5) = -x-5

Donc : abs(x) + abs (x-2) = abs(x+5) peut s'écrire :
-x + 2 - x = -x - 5
-x = -7
x = 7 ... mais x = 7 n'est pas compris dans ]-oo ; -5] ... et donc ne convient pas.

2°) Pour x compris dans [-5 ; 0], on a :
abs(x) = -x
abs(x-2) = 2-x
abs(x+5) = x + 5

Donc : abs(x) + abs (x-2) = abs(x+5) peut s'écrire :
-x + 2 - x = x + 5
-3x = 3
x = -1
Comme x = -1 est compris dans [-5 ; 0], x = -1 est solution.

Continue pour les 2 intervalles de x restant ...

---

EDIT

Pas vu le message mtschoon avant d'envoyer le mien.

[Hakim93]

Bonjour
Désolé pour la formule de politesse. Un oubli sans doute.
J'ai trouvé 2 solutions : -1 et 7 comme une équation de seconde degré
Donc peut-on transformer une équation de seconde degré en équation de degré 1 en utilisant les valeurs absolues ?
Et quel est le nombre maximal de solutions d'une équation de degré 1 avec les valeurs absolues.

[mtschoon]

@Hakim93, re-bonjour,

Bizarre de parler d'équation du second degré en classe de Troisième (programme français)...Peut-être t'es tu trompé de rubrique .

J'ignore la méthode que tu as utilisé.
Tu peux indiquer tes calculs si tu souhaites une vérification.

En utilisant la méthode usuelle relative à la suppression des valeurs absolues, les solutions sont bien -1 et 7.

[mtschoon]

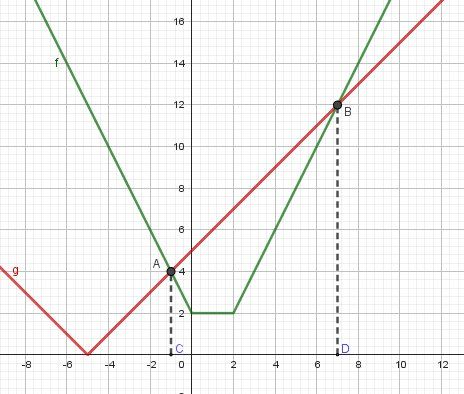
Illustration graphique.

$f(x)=|x|+|x-2|$
$g(x)=|x+5|$

Les solutions de (E) sont les abscisses des points A et B d'intersection des représentations graphiques de f et de g