étude de fonction racines carrées

bonsoir j'ai un exercice que je n'arrive pas à comprendre certaines parties.
soit la fonction f définie par f(x)=√(x²-6x+5)

détermine l'ensemble de définition de f
étudie les variations de la fonction f et dresse son tableau de variation
réponse
pour cette question il faut que x²-6x+5>0
quand j'applique le discriminant je trouve deux valeurs 1 et 5 donc l'ensemble de définition est]-∞ ;1]∪[5;+∞[
pour la deuxième question j'ai fait la dérivé de la fonction f et j'ai trouvé f'(x)=2x-6/2√(x²-6x+5)=x-3/√(x²-6x+5)
maintenant comme le dénominateur est positif donc le signe de f'(x) dépend du numérateur.
arrivé à ce niveau je bloque un peu je sais pas comment faire mon tableau de variation.

@Maxime-174 , bonjour,

$f(x)=x2−6x+5f(x)=\sqrt{x^2-6x+5}$

Condition d'existence : $x2−6x+5≥0x^2-6x+5\ge 0$
L'ensemble de définition est bien, comme tu l'indiques :
$Df=]−∞,1]∪[5,+∞[D_f=]-\infty,1]\cup[5,+\infty[$

$f′(x)=x−3x2−6x+5f'(x)=\dfrac{x-3}{\sqrt{x^2-6x+5}}$
L'ensemble de dérivabilité est :
$Df′=]−∞,1[∪]5,+∞[D_{f'}=]-\infty,1[\cup]5,+\infty[$

Effectivement, sur $D_{f'}$ , $f^{'} (x)$ est du signe de $(x - 3)$

1er cas : $x<1x\lt 1$ , donc à forciori, $x<3x\lt 3$ donc $x−3<0x-3\lt 0$ donc $f′(x)<0f'(x)\lt 0$ donc f strictement décroissante

2ème cas : $x>5x\gt 5$ donc à forciori $x>3x\gt 3$ donc $x−3>0x-3\gt 0$ donc $f(x)>0f(x)\gt 0$ donc f strictement croissante

Le tableau de variation s'en déduit.

@Maxime-174

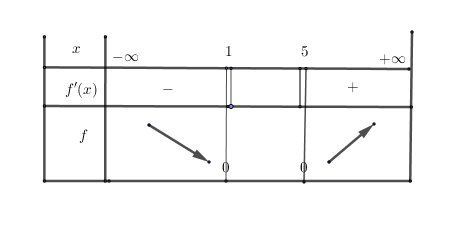
Tu peux compléter ce tableau avec les limites de $f$ en $+∞+\infty$ et $−∞-\infty$

@Maxime-174

Illustration graphique

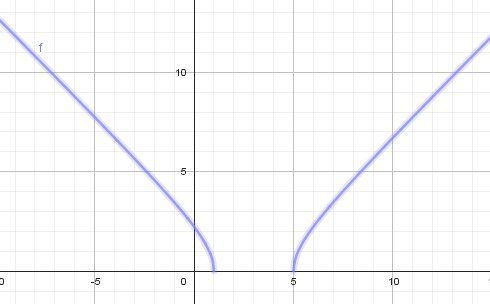
Bien sûr, cette étude peut être complétée par la recherche de tangentes "verticales", asymptotes "obliques".

@mtschoon bonsoir
Merci beaucoup

De rien @Maxime-174 et bon travail.