Résolution d'une équation diophantienne

Bonjour j'envoi ce message parce que j'aurai besoin d'un peu d'aide pour préparer un exercice particulier (je dois corrigé des réponses d'élèves) voici l'exercice :

Une troupe d'hommes et de femmes a dépensé dans une auberge 1000 sous. Les hommes ont payé 19 sous chacun, les femmes 13. Combien y avait-il d'hommes et de femmes?
Extrait des Éléments d'algèbre d'Euler.

Réponses de trois élèves de terminale Option Mathématiques expertes

Élève 1
Soit x le nombre d'hommes et y le nombre de femmes, on aura l'équation 19x+13y = 1000.
Cela donne y=
1000-19.x 13
12-6x
=76-x+
13
Par conséquent 12-6x est divisible par 13, donc 2-x l'est.
D'où x=2 car 2-x est un entier naturel donc positif et par conséquent y = 74.
Il y avait donc 2 hommes et 74 femmes, j'ai vérifié, ça marche.

Élève 2
J'ai écrit l'algorithme ci-dessous et je l'ai testé:
pour x allant de 1 à 52 faire
pour y allant de 1 à 52 faire
si 19x+13y = 1000 alors Afficher (x, y)
fin
fin
fin
J'obtiens comme affichage: (28,36) et (41,17).
J'ai vérifié ces résultats et c'est bon mais je ne pense pas que ce soit une démonstration.

Les questions à traiter

Analyser la réponse des trois élèves en mettant en évidence leurs réussites ainsi que leurs erreurs. Vous préciserez l'accompagnement que vous pouvez leur proposer.
Proposer une correction de l'exercice telle que vous l'exposeriez devant une classe de terminale Option Mathématiques Expertes.

Je viens de découvrir l'exercice mais ce que l'élève 1 a trouvé me parait correct, il a considéré que les x représente les hommes, et les y les femmes, et suite il a voulu faire une décomposition des nombres on dirait.

@Marvin , bonjour,

Ce n'est pas un système, car, d'après l'énoncé donné, il y a une seule équation avec deux inconnues
19x+13y = 1000.
Cela donne $y=−1913x+100013y=-\dfrac{19}{13}x+\dfrac{1000}{13}$
Soit $f$ définie par $f (x) = y$

Doit $f(x)=−1913x+100013f(x)=-\dfrac{19}{13}x+\dfrac{1000}{13}$

Pour $x≥0x\ge 0$ et $y≥0y\ge 0$ , il y a 4 couples de valeurs entières $(x, y)$ solutions.
$(2,47),(15,55),(28,36),(41,17)\boxed{(2,47), (15,55), (28,36), (41,17)}$

Ce sont les coordonnées des points $A, B, C, D$ du graphique.
(on peut les trouver facilement avec calculette ou tableur)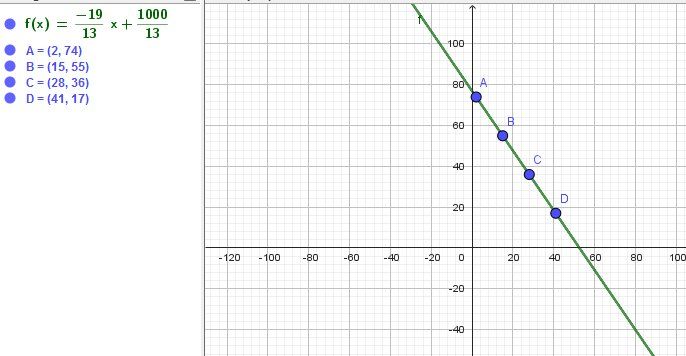

S'il s'agit d'un exercice d'arithmétique, il faut résoudre une équation diophantienne de la forme $a x + b y = c$

Voir une vidéo ici :
https://www.youtube.com/watch?v=XpYK-F4hX24
(Vu que tu parles d'élèves de l'option Maths Expertes, je pense qu'ils connaissent cette méthode)

Bonjour,

Une manière parmi d'autres de trouver les solutions :

1000 = 19h + 13f

h = (1000-13f)/19
h = (988 + 12 - 19f + 6f)/19
h = 52 - f + 6*(2 + f)/19

Il faut donc que (2+f) soit divisible par 19
f = 17 + 19 k (avec k entier) convient donc.

et h = (1000-13f)/19 = (1000 - 13 * (17 + 19k))/19
h = 41 - 13k

k = 0 --> f = 17 et h = 41
k = 1 --> f = 36 et h = 28
k = 2 --> f = 55 et h = 15
k = 3 --> f = 74 et h = 2

Il n'y a pas d'autres solutions, car f et h doivent évidemment être > 0

Merci beaucoup à vous deux!!!
Je ne vais pas vous citer pour ne pas rallonger la discussion mais les deux méthodes sont intéressante. La première , on obtient A,B,C,D qui sont 4 point "quelconques" de la droite.
La deuxième méthode j'avais jamais encore vu ça.
Du coup le deuxième élève ne s'était pas trop trompé (sauf le 52 qu'il aurai du remplacer pas 76 à un moment). Le premier élève a trouver le x =2 mais le y associé était 47 pas 74.(il a du inversé les chiffre), il a trouvé un couple mais il restait encore 3 couple

C'est très bien @Marvin si les diverses solutions proposées t'ont permis de solutionner ton exercice.