Exercice sur la récurrence
-
Noé Pradelles dernière édition par Noé Pradelles
Bonjour j'ai des difficulté pour cet exercice :
Exercice 3 :
Démontrer par récurrence que pour tout entier naturel 𝑛, on a :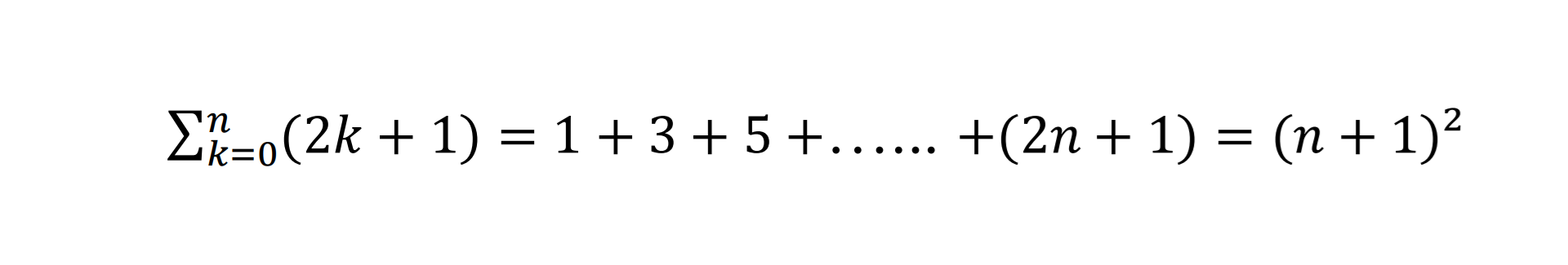
Voici ce que j'ai déjà fais mais je suis bloqué :
Initialisation : ∑ (2𝑘 + 1) = 1
(0+1)² = 1 donc la propriété est vraie pour n = 0.
Hérédité : On suppose que la propriété est vraie pour un entier n ≥ 0 :
1 + 3 + 5 + …... +(2𝑛 + 1) = (𝑛 + 1)²
-
BBlack-Jack dernière édition par
Bonjour,
S(n) = (n+1)²
S(n+1) = S(n) + (2*(n+1)+1)
S(n+1) = (n+1)² + (2n+3)
S(n+1) = (n²+2n+1+2n+3)
S(n+1) = n² + 4n + 4
S(n+1) = (n+2)²
S(n+1) = ((n+1) + 1)²Donc si S(n) = (n+1)² est vrai pour une valeur de n ... c'est encore vrai pour (n+1)
...
-
Noé Pradelles dernière édition par Noé Pradelles
@Black-Jack Je ne comprends pas, pourquoi "S(n)" ?
-
BBlack-Jack dernière édition par
@Black-Jack a dit dans Exercice sur la récurrence :
S(n)
SnS_nSn représente la somme depuis k = 0 jusque n de ... : Σk=0n(2k+1)\Sigma_{k=0}^n (2k+1)Σk=0n(2k+1)
et Sn+1S_{n+1}Sn+1 représente la somme depuis k = 0 jusque (n+1) de ... : Σk=0n+1(2k+1)\Sigma_{k=0}^{n+1} (2k+1)Σk=0n+1(2k+1)