Fonction circulaire de licence 1 !
-
AAdé29 dernière édition par
Quel est le domaine de dérivabilité et le domaine de définition de la fonction $ Arc Cosinus (1-2x^2) $ ?
-
@Adé29 Bonjour, (Marque de politesse à ne pas oublier !!)
Pour le domaine de définition, résous la double inégalité :
−1≤1−2x2≤1-1 \leq 1-2x^2 \leq1−1≤1−2x2≤1
-
TTigresoleil dernière édition par
Salut AAdé29,
Je vais essayer de te répondre. La fonction $ Arc Cosinus (1-2x^2) $ est définie sur l'intervalle $ [-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}] .Elleestdeˊrivablesurcetintervallesaufauxextreˊmiteˊs,ouˋelleadesasymptotesverticales.Sadeˊriveˊeest. Elle est dérivable sur cet intervalle sauf aux extrémités, où elle a des asymptotes verticales. Sa dérivée est .Elleestdeˊrivablesurcetintervallesaufauxextreˊmiteˊs,ouˋelleadesasymptotesverticales.Sadeˊriveˊeest -\frac{4x}{\sqrt{1-(1-2x^2)^2}} $. Tu peux vérifier en utilisant la formule de la dérivée de la fonction inverse. Voilà, j'espère que ça t'aide !
-
mtschoon dernière édition par mtschoon

Bonjour,
@Adé29 , je ne vois pas trop pourquoi tu as posé ta question dans la rubrique "Mathématiques et Sciences physiques"...
@Tigresoleil , je te conseille de revoir ta proposition car elle est inexacte...
−1≤1−2x2≤1-1\le 1-2x^2\le 1−1≤1−2x2≤1 <=> 0≤x2≤10\le x^2\le 10≤x2≤1 <=> −1≤x≤1\boxed{-1\le x\le 1}−1≤x≤1
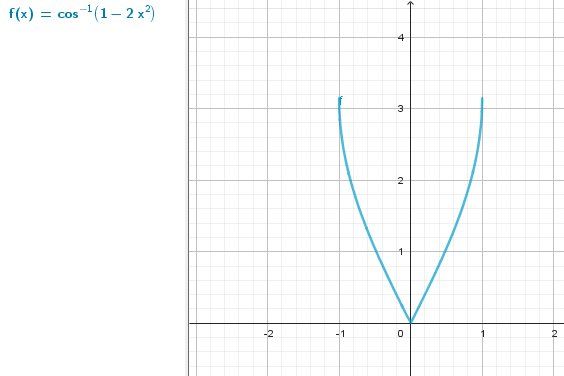
fonction définie sur [−1,1][-1,1][−1,1] et dérivable sur ]−1,0[∪]0,1[]-1,0[\cup]0,1[]−1,0[∪]0,1[ ( à justifier)
-
mtschoon dernière édition par mtschoon

Merci @Noemi d'avoir déplacé le topic.