4. Géométrie synthétique, triangle rectangle, problème

Géométrie synthétique, triangle rectangle, problème

  • -lala-o

    Bonjour, voici le problème :
    Soient A et B deux points sur un cercle C de centre O. Si C est un point du segment [AB], montrer que |OB|² - |OC|² =|AC|. |CB|.

  • mtschoon

    @srhmrc , bonjour,

    Je suppose que les symboles de valeurs absolues que tu utilises veulent dire "distance" entre deux points.
    Il faudra indiquer si c'est bien cela.

    Dans ma réponse, j'utilise les notations usuelles :
    [AB][AB][AB] veut dire segment
    ABABAB veut dire distance
    AB‾\overline {AB}AB veut dire mesure algébrique (lorsque A et B sont sur une droite orientée)
    voir :https://fr.wikipedia.org/wiki/Mesure_algébrique

    Un schéma pour éclairer :
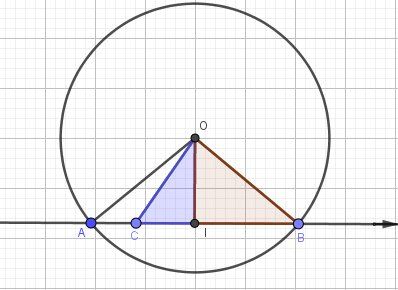
    puissance.jpg

  • B

    Bonjour
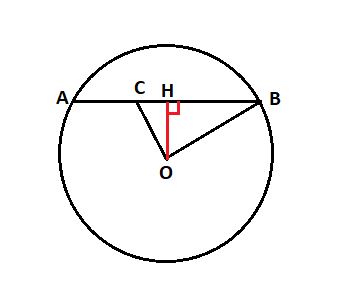
    OB² = OH² + HB²
    OC² = OH² + HC²
    OB² - OC² = HB²-HC²
    OB² - OC² = (CB-HC)²-HC²
    OB² - OC² = CB² + HC² - 2CB.HC - HC² = CB² - 2.CB.HC
    OB² - OC² = CB.(CB - 2HC)
    OB² - OC² = CB.((CB - HC) - HC) = CB.(HB-HC)

    Or HB = AH car ...

    Et donc : OB² - OC² = CB.(AH - HC)
    OB² - OC² = CB.AC

    CQFD.

    Sans titre.png

  • mtschoon

    @srhmrc ,

    Quelques pistes à approfondir et expliciter.

    Dans le schéma que je t'ai donné, III est le milieu de [AB][AB][AB]

    a) En utilisant le théorème de Pythagore dans les triangles rectangles OBIOBIOBI et OCIOCIOCI, on obtient :

    OB2−OC2=(OI2+IB2)−(OI2+IC)2)OB^2-OC^2=(OI^2+IB^2)-(OI^2+IC)^2)OB2−OC2=(OI2+IB2)−(OI2+IC)2)
    d'où , après simplifications
    OB2−OC2=IA2−IC2\boxed{OB^2-OC^2}=IA^2-IC^2OB2−OC2​=IA2−IC2

    b) En orientant la droite (AB)(AB)(AB) pour utiliser les mesures algébriques, avec la relation de Chasles on obtient :

    AC‾×CB‾=(AI‾+IC‾)(CI‾+IB‾)\overline{AC}\times \overline{CB}=(\overline{AI}+\overline{IC})(\overline{CI}+\overline{IB})AC×CB=(AI+IC)(CI+IB)
    AC‾×CB‾=(−IA‾+IC‾)(−IC‾−IA‾)\overline{AC}\times \overline{CB}=(\overline{-IA}+\overline{IC})(-\overline{IC}-\overline{IA})AC×CB=(−IA​+IC)(−IC−IA)
    d'où , après simplifications
    AC‾×CB‾=IA2−IC2\boxed{\overline{AC}\times \overline{CB}}=IA^2-IC^2AC×CB​=IA2−IC2

    Tu peux déduire: AC‾×CB‾=OB2−OC2\overline{AC}\times \overline{CB}=OB^2-OC^2AC×CB=OB2−OC2 puis la propriété demandée en prenant les distances.

    Remarque non demandée :
    Cet exercice fait penser à la "puissance" du point C par rapport au cercle qui est CA‾×CB‾=CO2−R2\overline{CA}\times \overline{CB}=CO^2-R^2CA×CB=CO2−R2 en appelant RRR le rayon du cercle.
    C'est à cela qu'a dû penser la personne qui a écrit l'énoncé...

  • mtschoon

    Bonjour @Black-Jack ,

    Je tapais ma réponse (en Latex, donc long à taper) pendant que tu enregistrais la tienne et je ne l'avais pas vu...

    Je te laisse traiter l'autre topic de @srhmrc qui n'a pas encore de réponse pour éviter les interférences.

Se connecter pour répondre