La distance terre lune/Tangentes

Bonjour j’ai besoin d’aide pour ces deux exercices merci d’avance !

l)Deux astronomes veulent effectuer une mesure précise de la distance Terre-Lune.
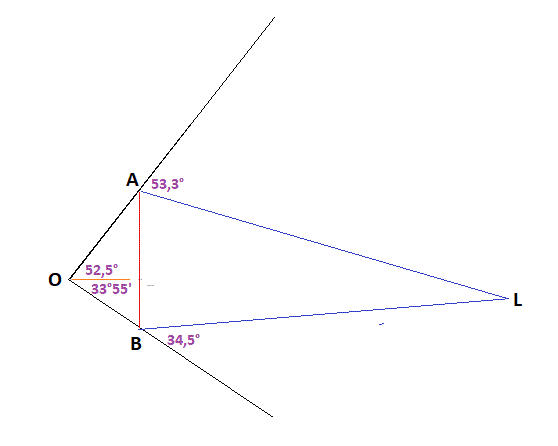
Le premier se place à Berlin en Allemagne (point A), le second au Cap de Bonne-Espérance en Afrique du Sud (au point B). Chacun de leur côté, ils mesurent, au même moment, depuis leur position, l'angle entre la direction du zénith (à la verticale de leur position) et la direction donnée par le centre de la face apparente de la Lune (le point L), ils trouvent ainsi les mesures a et 3.
On donne :
• rayon terrestre OA = OB = 6378 km avec O le centre de la Terre ;
• latitude de Berlin 52°30' N
• latitude du Cap 33°55' S (on supposera que les deux villes sont situées sur le même méridien) ;
• a = 53,3° et 3 = 34,5°.

Calculer la mesure de l'angle AOB (arrondie au dixième de degré).
Calculer la distance AB (arrondie au km).
Calculer les mesures des angles du triangle ALB (arrondies au dixième de degré).
Calculer les distances LA et LB (arrondies au km).
En déduire la longueur OL (arrondie au km).

ll) Le but de l'exercice est de construire avec précision les deux tangentes au cercle C passant par le point B et d'évaluer sous quel angle est vu le cercle C depuis le point B.
On se place dans un repère orthonormé du plan. Soit C le cercle de centre A(-5; 2) et de rayon 5. Soit B le point de coordonnées (6 ; 0).

Dessiner la figure en prenant le cm comme unité. La figure sera complétée au fur et à mesure.
Déterminer une équation cartésienne du cercle C.
Si on note E et F les points de contact avec le cercle des deux tangentes au cercle C passant par le point B, montrer que les points E et F sont situés sur le cercle C' de diamètre [AB]. Tracer le cercle C" et placer les points E et F.
Déterminer par le calcul les coordonnées des points E et F intersections des cercles C et C".
Vérifier à l'aide d'un calcul de produit scalaire que les droites (BE) et (BF) sont bien les tangentes cherchées.
Calculer les distances BE et BF, puis le produit scalaire BE. BF.
En déduire la valeur de l'angle (arrondie au dixième de degré) sous lequel le cercle est vu depuis le point B.

@zita Bonjour,

Un seul exercice par post. Ouvre un autre sujet pour le deuxième exercice.

Pour le premier exercice, indique tes éléments de réponse et la question qui te pose problème.

Bonjour,

I)

Rien ne permet dans l'énoncé de l'exercice de dire que le point L est dans le même plan que O,A et B.

On va (gratuitement) le supposer, sinon on ne peut pas donner de réponses chiffrées.

Angle(AOB) = 52,5° + 33°55'
Angle(AOB) = 52,5 + 33 + 55/60 = 86,4° (à moins de 0,1° près)

Par AlKashi
AB² = 2R²-2R².cos(AOB)
AB = 8733 km

angle(OAB) = 90°-52,5° = 37,5°
Angle(BAL) = 180° - 37,5° - 53,3° = 89,2°

angle(OBA) = 90°-33°55' = 56,0833°
angle(ABL) = 180 - 56,0833 - 34,5 = 89,4°

Angle(ALB) = 180 - 89,2 - 89,4 = 1,4°

Loi des sinus dans triangle ABL:
AB/sin(ALB) = AL/sin(ABL) = BL/sin(BAL)

8733/sin(1,4°) = AL/sin(89,4°) = BL/sin(89,2°)

AL = 357419 km
BL = 357404 km

Alkashi dans triangle OAL :
OL² = OA² + AL² -2.OA.AL.cos(OAL)
OL² = 6378² + 357419² - 26378357419*cos(56,0833°+89,2°)

OL = 362680 km
'''''''''''''''''''''
Il faudrait refaire les calculs en n'utilisant pas les valeurs arrondies (comme je l'ai fait par paresse) et en n'arrondissant que sur le calcul final.
Sans titre.png