Calcul d'une intégrale double
-
medou coulibaly dernière édition par Noemi

Bonjour je bloque sur cet exercice, j'ai besoin d'aide.On me demande de calculer l'intégrale
D = ((x,y) ∈ ℝ² ; 0 ≤ x ≤ 1 , 0 ≤ y ≤ x ) , f(x,y) = 1 / ( 1+x² )( 1+y² )
-
@medou-coulibaly Bonjour,
Indique l'expression des primitives de 11+x2\dfrac{1}{1+x^2}1+x21 ?
-
medou coulibaly dernière édition par

@Noemi sa primitive est : arctan(x)
-
Oui arctan(x)+Ctearctan(x) + Ctearctan(x)+Cte
Il te reste à calculer les primitives de arctan(x)1+x2\dfrac{arctan(x)}{1+x^2}1+x2arctan(x)
-
medou coulibaly dernière édition par

@Noemi j'ai trouvé comme primitive 1/2 arctan(x)^2
-
C'est correct attention à l'écriture : (arctan(x))22\dfrac{(arctan(x))^2}{2}2(arctan(x))2
-
medou coulibaly dernière édition par

@Noemi oui je suis bloqué je fais comment maintenant
-
La dernière primitive correspond au résultat de l'intégrale en faisant varier xxx de 0 à 1.
-
mtschoon dernière édition par mtschoon

Bonjour,
@medou-coulibaly a dit dans Calcul de triple intégrale :
Bonjour je bloque sur cet exercice, j'ai besoin d'aide.On me demande de calculer l'intégrale
D = ((x,y) ∈ ℝ² ; 0 ≤ x ≤ 1 , 0 ≤ y ≤ x ) , f(x,y) = 1 / ( 1+x² )( 1+y² )@medou-coulibaly , je ne comprends guère ton titre "triple intégrale"...
Il semble qu'il s'agisse d'une intégrale double.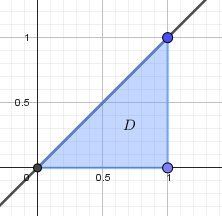
Vu que la borne yyy dépend de xxx, et que xxx varie de 000 à 111, il faut commencer par l'intégration par rapport à yyy et terminer par l'intégration par rapport à xxx
Je t'indique quelques pistes quil faut expliciter
I=∫x=01[∫y=0x1(1+x2)(1+y2)dy]dx\displaystyle I=\int_{x=0}^1\biggr[\int_{y=0}^x \dfrac{1}{(1+x^2)(1+y^2)}dy\biggr]dxI=∫x=01[∫y=0x(1+x2)(1+y2)1dy]dx
Soit :
J=∫y=0x1(1+x2)(1+y2)dy=[Arctany1+x2]0x\displaystyle J=\int_{y=0}^x \dfrac{1}{(1+x^2)(1+y^2)}dy=\biggr[\dfrac{Arctan y}{1+x^2}\biggr]_0^xJ=∫y=0x(1+x2)(1+y2)1dy=[1+x2Arctany]0xDonc, après calcul :
J=Arctanx1+x2J=\dfrac{Arctan x}{1+x^2}J=1+x2Arctanx
Donc I=∫x=01Arctanx1+x2dx\displaystyle I=\int_{x=0}^1 \dfrac{Arctan x}{1+x^2}dxI=∫x=011+x2Arctanxdx
Tu fais le calcul de cette dernière intégrale et sauf erreur, tu dois trouver : I=π232\boxed{I=\dfrac{\pi^2}{32}}I=32π2
Bons calculs.
Reposte si ce n'est pas de cela dont il s'agit.
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Il faut aussi se méfier de l'ordre des intégration, x et puis y ou le contraire.
Et comme d'habitude, la convention d'écriture n'est pas la même pour tous ...
Juste pour info, voila par exemple les résultats ce que cela peut donner :
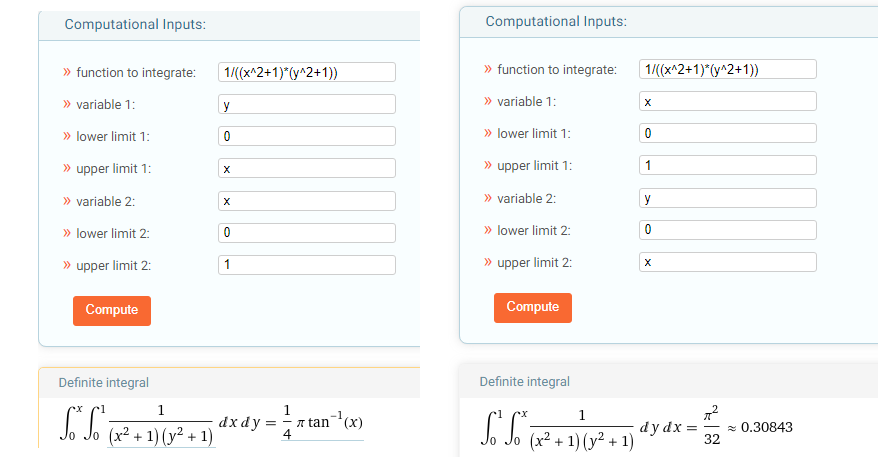
-
mtschoon dernière édition par mtschoon

Bonjour,
Personnellement, j'ai toujours fait la version 2 que tu indiques vu que yyy dépend de xxx et que xxx varie de 000 à 111 , et qui donne π232\dfrac{\pi ^2}{32}32π2
-
BBlack-Jack dernière édition par
Bonjour,
Oui ... mais quoi qu'il en soit, ce n'est pas la manière unique de comprendre les choses.
Chacun ses conventions (malheureusement)
Voila les résultats sur un autre site qui confirment que les conventions d'écritures sont loin d'être universelles.
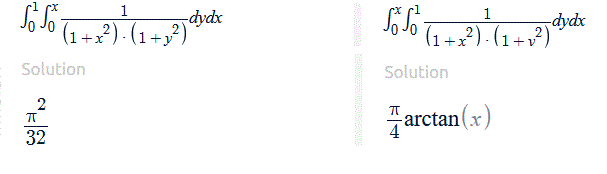
Personnellement, dans mon boulot, je n'ai pas de soucis.
Quand j'ai une intégrale double à calculer, j'ai du l'établir à partir d'un problème Physique et je connais donc la manière pour l'interpréter.Mais quand on me donne une intégrale double hors contexte (comme dans un exercice de Math pur et dur), j'ai souvent un gros doute sur l'interprétation à lui donner ... comme on le voit dans les exemples de solutions données par les 2 logiciels mis en exemple.
Chacun pensant évidemment que son interprétation du problème est la bonne ...
-
mtschoon dernière édition par mtschoon

@medou-coulibaly nous dira peut-être ce qu'en pense son professeur de mathématiques.
-
BBlack-Jack dernière édition par
@mtschoon a dit dans Calcul de triple intégrale :
@medou-coulibaly nous dira peut-être ce qu'en pense son professeur de mathématiques.
Oui, il aura une des deux visions possibles ... qu'il pensera être la seule bonne.

-
mtschoon dernière édition par mtschoon

je trouve que l'on perd notre temps...
C'est le professeur qui juge (et ce n'est ni toi, ni moi...)Personnellement, j'arrête ici cette discussion

-
BBlack-Jack dernière édition par
Pas de soucis pour moi,
Il y a l'école et le professeur qui a toujours raison.
Et puis il y a la vraie vie où on doit calculer ce que le problème réel (physique) impose ... et qui trop souvent a des conséquences "hasardeuses" parce que le matheux a qui on confie les calculs n'a pas les mêmes conventions que celui qui établit l'équation traduisant la physique du problème et sous-traite ensuite le travail de résolution mathématiques.
J'arrête donc aussi la discussion, bien que le problème reste bien réel.

-
medou coulibaly dernière édition par

@mtschoon Bonjour madame effectivement c'est ce que je trouve pi^2 /32
-
medou coulibaly dernière édition par

@mtschoon oui madame c'est ce qu'on trouve
-
medou coulibaly dernière édition par

@Black-Jack Bonjour la première image c'est ce que je trouve et la seconde ce n'est pas çà
-
medou coulibaly dernière édition par

@medou-coulibaly je veux changer par integrale multiple
Mais voilà ce que ça me montre
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , bonjour,
Peut-être que pour modifier un titre il faut avoir les droits de modérateur...
La modération le fera peut-être.@medou-coulibaly a dit dans Calcul de triple intégrale
@mtschoon Bonjour madame effectivement c'est ce que je trouve pi^2 /32
C'est bien @medou-coulibaly
Ton calcul est exact.
Ton professeur te dira si c'est ce qu'il voulait (je suis convaincue que c'est cela qu'il veut ...mais ce serait bien d'en avoir la certitude...)
-
mtschoon dernière édition par mtschoon

Merci @Noemi d'avoir modifié le titre.
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame, c'est ce que j'ai fait et j'ai présenté au prof et il dit ça lui-même il trouve.il dit j'ai bien travaillé. Merci

-
mtschoon dernière édition par mtschoon

@medou-coulibaly a dit dans Calcul d'une intégrale double :
@mtschoon Bonjour madame, c'est ce que j'ai fait et j'ai présenté au prof et il dit ça lui-même il trouve.il dit j'ai bien travaillé. Merci

C'est parfait @medou-coulibaly !