Nombres complexes maths expertes
-
Vvittoriaisadora dernière édition par
Bonjour je n’arrive pas a résoudre la 2eme question de cet énoncé : (j’y joins également la première question qui est censée aider)
- Déterminer la forme algébrique de (1+ i)(1+2i) (1+3i)
- En déduire la valeur de arctan(1)+arctan(2)+arctan(3)
Merci d’avance !!
-
mtschoon dernière édition par mtschoon

@vittoriaisadora , bonjour,
Pour la question 1 ), tu as dû trouver :
(1+i)(1+2i)(1+3i)=−10(1+i)(1+2i)(1+3i)=-10(1+i)(1+2i)(1+3i)=−10Pistes à expliciter avec rigueur pour la 2) (il n'y a que les idées, j'ai fait vite...)
L'argument principal de −10-10−10 est π\piπ vu que −10-10−10 est un réel strictement négatif.
arg[(1+i)(1+2i)(1+3i)]=πarg[(1+i)(1+2i)(1+3i)]=\piarg[(1+i)(1+2i)(1+3i)]=π
arg(1+i)+arg(1+2i)+arg(1+3i)=π\boxed{arg(1+i)+arg(1+2i)+arg(1+3i)=\pi}arg(1+i)+arg(1+2i)+arg(1+3i)=π
Cercle trigonométrique :
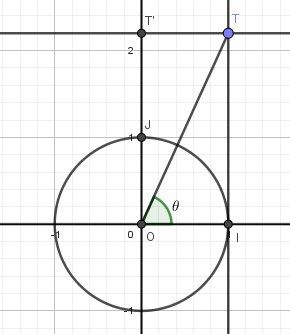
Pour tout θ\thetaθ compris entre −π2-\dfrac{\pi}{2}−2π et +π2+\dfrac{\pi}{2}+2π
arg(1+iθ)=Arctanθarg(1+i\theta)=Arctan\thetaarg(1+iθ)=ArctanθTu prends θ=1\theta=1θ=1 , θ=2\theta=2θ=2 et θ=3\theta=3θ=3 et tu dois trouver la propriété demandée.