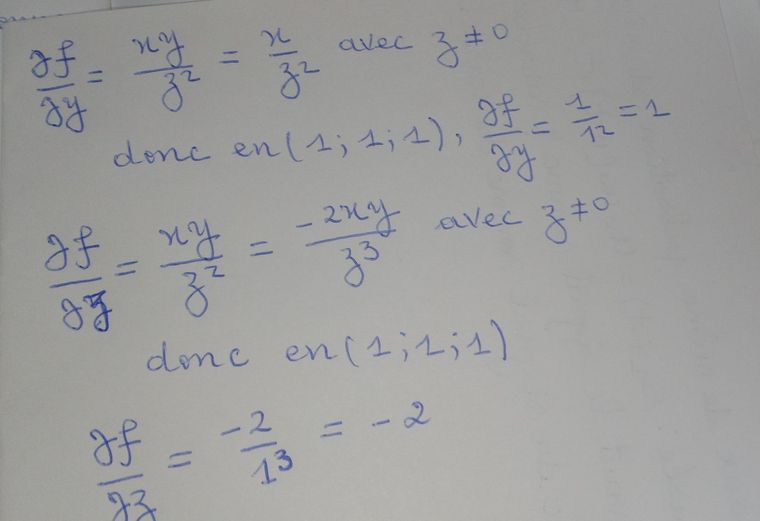Dérivées partielles et différentielles d'une fonction
-
medou coulibaly dernière édition par

Bonsoir je bloque sur cet exercice, après plusieurs tentatives, je n'y arrive pas à trouver une issue.
Soit f : (x,y,z) ==> { f (x,y,z) = xy/z^2 lorsque z ≠ 0 , f( x,y,z ) = 0
1/
Calculer les 3 dérivées partielles de f dans la base canonique de ℝ³ au point (1,1,1)
2 ) Montrer ensuite que f est différentiable en (1,1,1) , f est-elle différentiable en ( 0,0,0 )
-
@medou-coulibaly Bonsoir,
Pour le calcul de la dérivée partielle de fff par rapport à xxx, tu considères que yyy et zzz sont des constantes.
Même principe pour les autres dérivées partielles.Si tu as compris les exercices précédents, tu es capable de calculer les dérivées partielles.
Indique tes calculs.
-
medou coulibaly dernière édition par

@Noemi Bonsoir Monsieur
Regarde cette définition il s'agit ? J'ai des difficultés à l'appliquer
-
medou coulibaly dernière édition par

@medou-coulibaly
∂xf( y, z ) = y / yz^2
∂yf ( x, z ) = x/ z^2
∂zf( x, y ) = xy / 2zy
vérifiez svp
-
Attention à l'écriture, c'est f(x,y,z)f(x,y,z)f(x,y,z)
Vérifie la première et la troisième.
-
medou coulibaly dernière édition par medou coulibaly

@Noemi
∂xf( x,y, z ) = y / yz^2
∂xf ( x,y, z ) = x/ z^2
∂xf( x, y, z ) = xy / 2zy
Bonjour revérifier
-
Re vérifie.
Si xxx est la variable et aaa une constante :
La dérivée de axaxax est aaa
La dérivée de ax2\dfrac{a}{x^2}x2a est −2ax3-\dfrac{2a}{x^3}−x32aTu calcules ensuite la valeur de ces dérivées au point de coordonnée (1;1;1)(1;1;1)(1;1;1).
-
BBlack-Jack dernière édition par
δfδx=yz2\frac{\delta f}{\delta x} = \frac{y}{z^2}δxδf=z2y ... si z est différent de 0
et donc en (1 ; 1 ; 1), δfδx=1\frac{\delta f}{\delta x} = 1δxδf=1
δfδy=...\frac{\delta f}{\delta y} = ... δyδf=... et donc en (1 ; 1 ; 1), δfδy=...\frac{\delta f}{\delta y} = ...δyδf=...
δfδz=...\frac{\delta f}{\delta z} = ... δzδf=... et donc en (1 ; 1 ; 1), δfδz=...\frac{\delta f}{\delta z} = ...δzδf=...
Attention, pour la dérivée en (0;0;0) il faut réfléchir un peu ...
-
medou coulibaly dernière édition par medou coulibaly

@Black-Jack
Non jusque-là je ne comprends pas cette affaire de dérivées partielles
Pour moi ∂f/∂y = x/z^2 puisque je dérive y en laissant x et z constant
Noemi si je veux bien comprendre si la dérivée de ax = a et aussi la dérivée de a/x^2 = - 2a / x^3
Alors ce que Black Jack a fait disant que ∂f/∂x = xy/z^2 = xy^2/ (z^2)^2 = xy^2/z^4 = x/z^2 d'où ∂f/∂x = x / z^2.
Je m'arrête là, personnellement j'ai des difficultés à m'ensortir car je ne me retrouve pas
-
La deuxième est juste, donc applique le même raisonnement pour les deux autres.
-
medou coulibaly dernière édition par

@Noemi cela est dû à quoi ?Screenshot_20240206_180105_Phoenix.jpg
-
BBlack-Jack dernière édition par Black-Jack
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
@Black-Jack
Non jusque-là je ne comprends pas cette affaire de dérivées partielles
Pour moi ∂f/∂y = x/z^2 puisque je dérive y en laissant x et z constant
Noemi si je veux bien comprendre si la dérivée de ax = a et aussi la dérivée de a/x^2 = - 2a / x^3
Alors ce que Black Jack a fait disant que ∂f/∂x = xy/z^2 = xy^2/ (z^2)^2 = xy^2/z^4 = x/z^2 d'où ∂f/∂x = x / z^2.
Je m'arrête là, personnellement j'ai des difficultés à m'ensortir car je ne me retrouve pasBonjour,
Je n'ai JAMAIS écrit les absurdités que tu me prêtes.
Je n'ai pas écrit :
"∂f/∂x = xy/z^2 = xy^2/ (z^2)^2 = xy^2/z^4 = x/z^2 d'où ∂f/∂x = x / z^2."mais bien ∂f/∂x = y/z² (si z est différent de 0) ... ce qui est correct.
Tu as écrit : ∂xf( x,y, z ) = y / yz^2 ... ce qui est faux.
∂f/∂y = x/z^2 est exact ... si z est différent de 0
et ta dérivée partielle de f par rapport à z est fausse.
-
medou coulibaly dernière édition par medou coulibaly

@Black-Jack
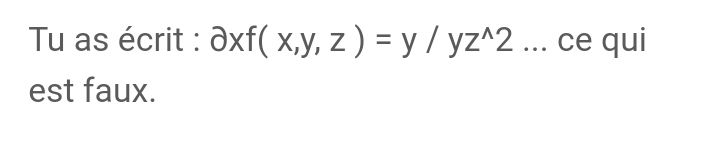
Ce qui est là aussi n'est pas mon écriture lisez bien ce que j'ai écrit, ne dites pas ce que j'ai pas écrit.
Je sais que je ne maîtrise pas bien l'exercice mais faites attention à ce que j'ai pas écrit
-
medou coulibaly dernière édition par

@Black-Jack

Si celle-ci alors j'avais déjà cela bien avant aujourd'hui
-
BBlack-Jack dernière édition par Black-Jack
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
@Black-Jack
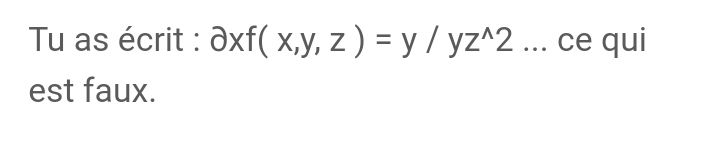
Ce qui est là aussi n'est pas mon écriture lisez bien ce que j'ai écrit, ne dites pas ce que j'ai pas écrit.
Je sais que je ne maîtrise pas bien l'exercice mais faites attention à ce que j'ai pas écritJ'ai fais un "copier-coler" de ce que tu as écrit dans ton message et que je refais ici :
∂xf( x,y, z ) = y / yz^2
∂xf ( x,y, z ) = x/ z^2
∂xf( x, y, z ) = xy / 2zyEt tu as bel et bien écrit ∂xf( x,y, z ) = y / yz^2 comme je l'ai mentionné.
Par contre, ce que tu as copié comme étant ma réponse ne correspond pas du tout à ce que j'ai écrit.
Pour f (x,y,z) = xy/z^2 si z est différent de 0.
f (x,y,z) = xy*z^-2
On a aussi (si z est différent de 0) : ∂f/∂z = xy * (-2)*z^(-3)soit : ∂f/∂z = -2xy/z³ ... ce n'est pas non plus ce que tu as écrit.
-
medou coulibaly dernière édition par

@medou-coulibaly si cela est vrai que pour dériver partiellement qu'il faut tenir compte des constantes et en dérivant dans l'ordre des variables alors
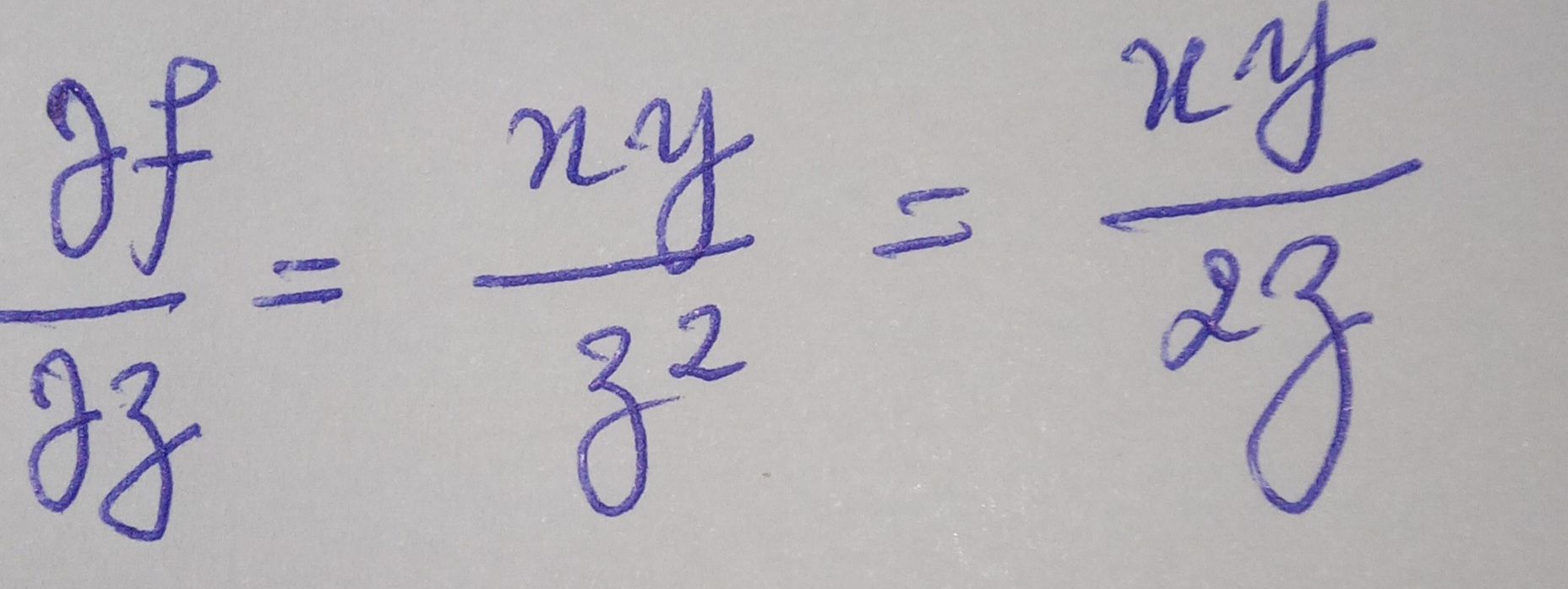 vérifié cela
vérifié cela
-
BBlack-Jack dernière édition par
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
@medou-coulibaly si cela est vrai que pour dériver partiellement qu'il faut tenir compte des constantes et en dérivant dans l'ordre des variables alors
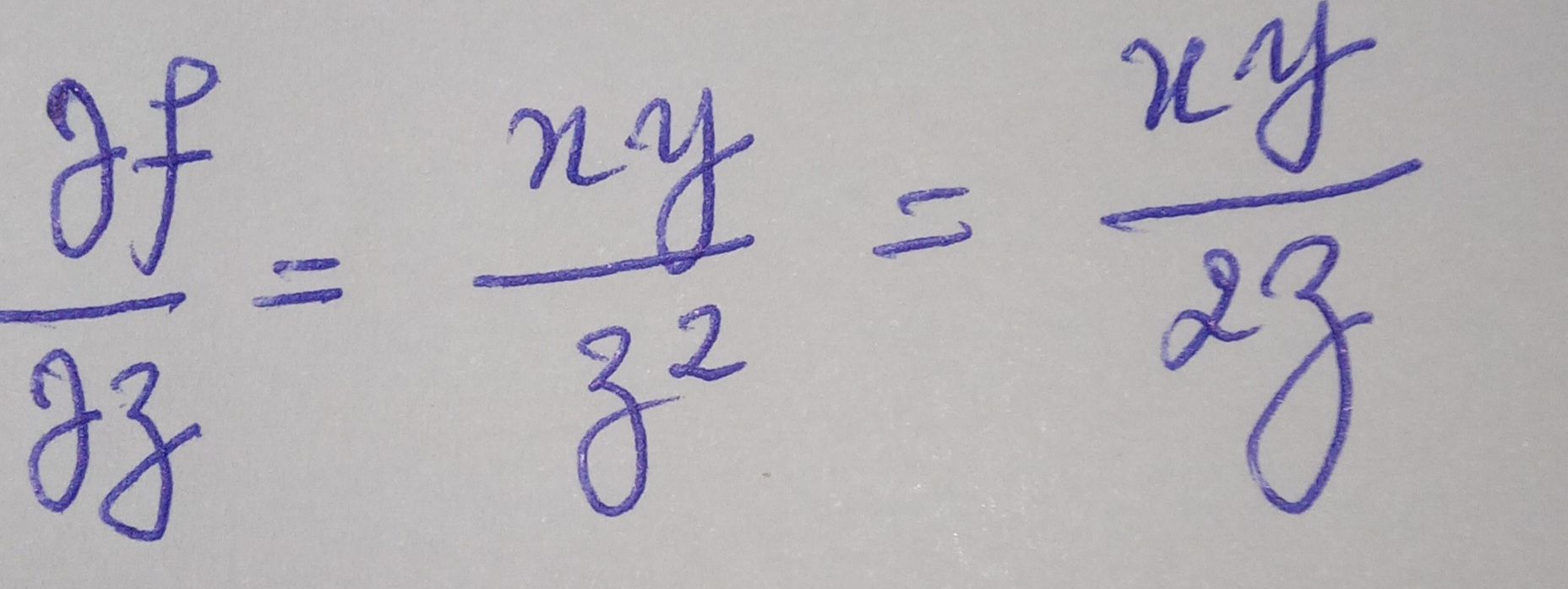 vérifié cela
vérifié celaAie aie aie.
La dérivée d'un quotient n'est pas le quotient des dérivées.
Voir mon message précédent.
-
medou coulibaly dernière édition par

@Black-Jack
Je sais ici que la fonction de la forme U/V avec V^2
-
medou coulibaly dernière édition par

@Black-Jack
Dans ma photo sur-soulignée par vous , vous dîtes que j'ai écrit y/yz^2
-
medou coulibaly dernière édition par

@Black-Jack je préfère abandonner l'exercice c'est mieux.Merci

-
BBlack-Jack dernière édition par Black-Jack
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
@Black-Jack
Je sais ici que la fonction de la forme U/V avec V^2Et bien alors, il suffit de dériver correctement :
Pour une dérivée partielle par rapport à z, x et y sont considérés comme des constantes.
Quelle est la dérivée par rapport à z de f(z) = A/z² (avec A = x.y = constante) ?
f '(z) = A * -(z²)'/z^4 = A * -2z/z^4 = -2A/z³
et comme A = xy ---> f'(z) = -2xy/z³Mais dans un tel cas, on n'utilise pas la notation f '(z), on ecrit :
∂f/∂z = -2xy/z³
-
BBlack-Jack dernière édition par
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
@Black-Jack
Dans ma photo sur-soulignée par vous , vous dîtes que j'ai écrit y/yz^2
JE N'AI JAMAIS ECRIT CELA
-
medou coulibaly dernière édition par

@Black-Jack
Le mieux pour moi est d'abandonner l'exercice, merci à vous
-
medou coulibaly dernière édition par

@Black-Jack * signifie quoi ?
-
BBlack-Jack dernière édition par
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
@Black-Jack * signifie quoi ?
Bonjour,
C'est un symbole de "multiplication" très souvent employé.
Pour écrire par exemple "a fois b", on peut écrire tout ce qui suit :
a∗ba * ba∗b
a.ba.ba.b
a×ba \times ba×b
abababChacune de ces écritures ayant des avantages et des inconvénients.
Le point dans l'écriture a.ba.ba.b peut parfois être confondu avec le point qui sépare la partie entière et décimale d'un nombre (1 fois 2, si on écrit 1.2 il y a risque de confusion)
Avec a×ba \times ba×b, on peut confondre le signe ×\times× avec la variable X
...
''''''''''''''''''''''''''''''
Je réécris en utilisant LatexQuelle est la dérivée par rapport à z de f(z)=Az2f(z) = \frac{A}{z^2}f(z)=z2A (avec A = x.y = constante) ?
f′(z)=A×−(z2)′z4=A×−2zz4=−2Az3f '(z) = A \times \frac{-(z^2)'}{z^4} = A \times \frac{-2z}{z^4} = -\frac{2A}{z^3}f′(z)=A×z4−(z2)′=A×z4−2z=−z32A
et comme A=xy→f′(z)=−2xyz3A = xy \to f'(z) = -\frac{2xy}{z^3}A=xy→f′(z)=−z32xyMais dans un tel cas, on n'utilise pas la notation f '(z), on ecrit :
∂f∂z=−2xyz3\frac{∂f}{∂z} = -\frac{2xy}{z^3}∂z∂f=−z32xy
-
medou coulibaly dernière édition par

@Black-Jack Bonjour j'ai compris cela merci beaucoup à vous maintenant je vais passer au ( 1 , 1 ,1 )
-
medou coulibaly dernière édition par

-
Attention au suite d'égale que tu écris.
∂f∂y(x,y,z)=xz2\dfrac{\partial f}{\partial y}(x,y,z)=\dfrac{x}{z^2}∂y∂f(x,y,z)=z2x∂f∂y(1,1,1)=112=1\dfrac{\partial f}{\partial y}(1,1,1)=\dfrac{1}{1^2}=1∂y∂f(1,1,1)=121=1
∂f∂z(x,y,z)=−2xyz3\dfrac{\partial f}{\partial z}(x,y,z)=\dfrac{-2xy}{z^3}∂z∂f(x,y,z)=z3−2xy
et
∂f∂z(1,1,1)=−2\dfrac{\partial f}{\partial z}(1,1,1)=-2∂z∂f(1,1,1)=−2
-
medou coulibaly dernière édition par medou coulibaly

@Noemi ok d'accord merci j'ai bien compris

Pour la 2)
J'ai besoin d'une explication simplifiée de la définition et du théorème de la différentiabilité d'une fonction
-
medou coulibaly dernière édition par

@medou-coulibaly jusque-là j'ai pas encore eu de réponse pour pouvoir avancer
-
medou coulibaly dernière édition par

@medou-coulibaly Bonjour je bloque toujours sur la question et je n'arrive pas à avancer
-
mtschoon dernière édition par

@medou-coulibaly , bonjour,
Comme je constate que tu n'as pas de réponse à tes deux dernières questions, je regarde.
A vrai dire ce topic étant tellement long et "bizarre", je préfère partir de ton énoncé, quitte à faire des répétitions.
@medou-coulibaly a dit dans Dérivées partielles et différentielles d'une fonction :
Bonsoir je bloque sur cet exercice, après plusieurs tentatives, je n'y arrive pas à trouver une issue.
Soit f : (x,y,z) ==> { f (x,y,z) = xy/z^2 lorsque z ≠ 0 , f( x,y,z ) = 0
1/
Calculer les 3 dérivées partielles de f dans la base canonique de ℝ³ au point (1,1,1)
2 ) Montrer ensuite que f est différentiable en (1,1,1) , f est-elle différentiable en ( 0,0,0 )Il semble manquer quelque chose dans ton énoncé.
f(x,y,z)=xyz2f(x,y,z)=\dfrac{xy}{z^2}f(x,y,z)=z2xy pour z≠0\boxed{z\ne 0}z=0 C'est OKPar contre , tu continue par f(x,y,z)=0f(x,y,z)=0f(x,y,z)=0 ...?
Je suppose que tu as voulu écrire f(x,y,z)=0f(x,y,z)=0f(x,y,z)=0 pour z=0\boxed{z=0}z=0
Vérifie.Pour la 1 ), on te demande de calculer les 3 dérivées partielles au point (1,1,1).
Tu as deux façons possibles, mais il faut savoir l'esprit de la question.
-
mtschoon dernière édition par mtschoon

Première façon : utiliser la définition
J'utilise les notations dont j'ai l'habitude.
a) dérivée partielle de f par rapport à xxx au point (1,1,1)
f(1,1,1)=1×112=1f(1,1,1)=\dfrac{1\times 1}{1^2}=1f(1,1,1)=121×1=1
f(1+h,1,1)=(1+h)(1)12=1+hf(1+h,1,1)=\dfrac{(1+h)(1)}{1^2}=1+hf(1+h,1,1)=12(1+h)(1)=1+hδfδx(1,1,1)=limh→0f(1+h,1,1)−f(1,1,1)h\displaystyle \dfrac{\delta f}{\delta x}(1,1,1)=\lim_{h\to 0}\dfrac{f(1+h,1,1)-f(1,1,1)}{h}δxδf(1,1,1)=h→0limhf(1+h,1,1)−f(1,1,1)
δfδx(1,1,1)=limh→01+h+1h=limh→0hh=1\displaystyle \dfrac{\delta f}{\delta x}(1,1,1)=\lim_{h\to 0}\dfrac{1+h+1}{h}=\lim_{h\to 0}\dfrac{h}{h}=\boxed{1}δxδf(1,1,1)=h→0limh1+h+1=h→0limhh=1
b) dérivée partielle de f par rapport à yyy au point (1,1,1)
f(1,1,1)=1f(1,1,1)=1f(1,1,1)=1
f(1,1+h,1)=(1)(1+h)12=1+hf(1,1+h,1)=\dfrac{(1)(1+h)}{1^2}=1+hf(1,1+h,1)=12(1)(1+h)=1+hComme ci-dessus, , tu trouves
δfδy(1,1,1)=limh→0f(1,1+h,1)−f(1,1,1)h=1\displaystyle \dfrac{\delta f}{\delta y}(1,1,1)=\lim_{h\to 0}\dfrac{f(1,1+h,1)-f(1,1,1)}{h}=\boxed{1}δyδf(1,1,1)=h→0limhf(1,1+h,1)−f(1,1,1)=1c) dérivée partielle de f par rapport à zzz au point (1,1,1)
f(1,1,1)=1f(1,1,1)=1f(1,1,1)=1
f(1,1,1+h)=(1)(1)(1+h)2=1(1+h)2f(1,1,1+h)=\dfrac{(1)(1)}{(1+h)^2}=\dfrac{1}{(1+h)^2}f(1,1,1+h)=(1+h)2(1)(1)=(1+h)21δfδz(1,1,1)=limh→0f(1,1,1+h)−f(1,1,1)h\displaystyle \dfrac{\delta f}{\delta z}(1,1,1)=\lim_{h\to 0}\dfrac{f(1,1,1+h)-f(1,1,1)}{h}δzδf(1,1,1)=h→0limhf(1,1,1+h)−f(1,1,1)
δfδz(1,1,1)=limh→01(1+h)2−1h\displaystyle \dfrac{\delta f}{\delta z}(1,1,1)=\lim_{h\to 0}\dfrac{\dfrac{1}{(1+h)^2}-1}{h}δzδf(1,1,1)=h→0limh(1+h)21−1
δfδz(1,1,1)=limh→0=1−(1+h)2(1+h)2×1h\displaystyle \dfrac{\delta f}{\delta z}(1,1,1)=\lim_{h\to 0}=\dfrac{1-(1+h)^2}{(1+h)^2}\times \dfrac{1}{h}δzδf(1,1,1)=h→0lim=(1+h)21−(1+h)2×h1
Tu développes le numérateur avec (1+h)2=1+2h+h2(1+h)^2=1+2h+h^2(1+h)2=1+2h+h2 et tu simplifies
Tu dois trouver :
δfδz(1,1,1)=limh→0−h2−2h(1+h)2h=limh→0h(−h−2)(1+h)2h\displaystyle \dfrac{\delta f}{\delta z}(1,1,1)=\lim_{h\to 0}\dfrac{-h^2-2h}{(1+h)^2h}=\lim_{h\to 0}\dfrac{h(-h-2)}{(1+h)^2h}δzδf(1,1,1)=h→0lim(1+h)2h−h2−2h=h→0lim(1+h)2hh(−h−2)Tu simplifies par hhh non nul, tu fais tendre hhh vers 000 et tu trouves :
δfδz(1,1,1)=−2\displaystyle \dfrac{\delta f}{\delta z}(1,1,1)=\boxed{-2}δzδf(1,1,1)=−2
-
mtschoon dernière édition par mtschoon

Seconde façon (qui a été vu au cours des réponses précédentes, je crois, donc je ne refais pas)
Tu calcules les 3 dérivées partielles à un point (x,y,z) avec les formules usuelles de dérivées et tu remplaces ensuite x,y,z par 1,1,1 dans les résultats.
Tu trouves bien sûr les même résultats qu'avec la définition
- Conséquence
Tu utilises les valeurs trouvées à la question 1 ).
Vu ue les 3 dérivées partielles existent en (1,1,1), la différentielle en (1,1,1) existe.
La différentielle de fff au point (1,1,1) est :
df(1,1,1)=(1)dx+(1)dy+(−2)dzdf(1,1,1) =(1) dx+(1)dy+(-2)dzdf(1,1,1)=(1)dx+(1)dy+(−2)dz
df(1,1,1)=dx+dy−2dz\boxed{df(1,1,1)= dx+dy-2dz}df(1,1,1)=dx+dy−2dzAu point (0,0,0)(0,0,0)(0,0,0), z=0z=0z=0 donc tu dois utiliser la seconde expression de f(x,y,z)f(x,y,z)f(x,y,z).
Tu peux prouver la non continuité fff en (0,0,0)(0,0,0)(0,0,0) donc fff non différentiable.
Ou bien , pour rester dans l'esprit de l'exercice, tu peux chercher les dérivées partielles en (0,0,0).
Pour δfδz(0,0,0)\dfrac{\delta f}{\delta z}(0,0,0)δzδf(0,0,0), tu dois trouver ±∞\pm \infty±∞ donc pas de dérivée partielle, donc fff non différentiable en (0,0,0)Bonnes réflexions.
-
medou coulibaly dernière édition par

@mtschoon

Bonjour Madame voici l'énoncé
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , bonjour,
Tu n'avais pas fait d'erreur de copie.
C'est l'énoncé qui n'est pas très explicite à mon goût.
Il faut faire la déduction soi-même.
donc, il faut comprendre f(x,y,z)=0f(x,y,z)=0f(x,y,z)=0 pour z=0z=0z=0
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame j'ai du mal à comprendre la définition de la différentielle et son théorème
-
mtschoon dernière édition par mtschoon

Ce que je t'écris n'est guère correct, mais tant pis...
Si ça peut te permettre de comprendre, c'est l'essentiel...Au voisinage du point (1,1,1) dans ton exercice, df représente une petite variation de fff, en fonction de dx (petite variation de x), de dy (petite variation de y) et dz (petite variation de z)
C'est la généralisation de ce que tu avais vu en Première/terminale pour les fonctions à une variable xxx (de RRR vers RRR).
je te conseille de consulter cette vidéo:
https://www.youtube.com/watch?v=VkylRwE0XMM
-
medou coulibaly dernière édition par

@mtschoon ok merci beaucoup madame j'ai repris et je me retrouve madame merci beaucoup à vous

-
mtschoon dernière édition par

De rien @medou-coulibaly .
Si maintenant c'est clair pour toi, c'est parfait.
-
medou coulibaly dernière édition par

@mtschoon
Merci beaucoup madame j'ai consulté la vidéo ça va , maintenant j'ai fait un nouveau poste dont j'ai de difficultés
-
mtschoon dernière édition par

OK @medou-coulibaly .
je pense qu'il s'agit de calcul d'un volume; Black-Jack a commencé à te répondre.
-
medou coulibaly dernière édition par

@mtschoon oui