Ecrire sans les valeurs absolues
-
medou coulibaly dernière édition par

Bonjour je bloque sur cet exercice j'ai besoin de votre aide.
Soit f(θ) = | cos²θ - sin²θ | pour θ ∈ ] - π , π [. Ecrire sans les valeurs absolues
-
@medou-coulibaly Bonjour,
Commence par écrire l'expression en fonction de cosθcos\thetacosθ, puis factorise l'expression, puis tableau de signes, puis .....
-
medou coulibaly dernière édition par

@Noemi j'ai du mal a exprimé en fonction de cosθ
-
medou coulibaly dernière édition par medou coulibaly

@Noemi je pense que | cos²θ - sin²θ | devient cos²θ - sin²θ = 0
-
mtschoon dernière édition par mtschoon

Bonjour,
@medou-coulibaly a dit dans Ecrire sans les valeurs absolues :
@Noemi je pense que | cos²θ - sin²θ | devient cos²θ - sin²θ = 0
Ce que tu indiques n'est pas bon.
Si tu souhaites transformer en cosθcos\thetacosθ, pense que cos2θ+sin2θ=1cos^2\theta+sin^2 \theta=1cos2θ+sin2θ=1 donc sin2θ=1−cos2θsin^2\theta=1-cos^2\thetasin2θ=1−cos2θ
Tu trouves donc que :
cos2θ−sin2θ=2cos2θ−1cos^2\theta-sin^2\theta=2cos^2\theta-1cos2θ−sin2θ=2cos2θ−1
-
medou coulibaly dernière édition par medou coulibaly

@mtschoon ok mais Néomi dit de factoriser
2cos^2-1 = cosθ ( 2cosθ - 1/cosθ )
-
BBlack-Jack dernière édition par
Bonjour,
L'énoncé n'est pas très directif et donc on pourrait faire ceci, sans l'ombre d'un calcul :
∣cos2(θ)−sin2(θ)∣=(cos2(θ)−sin2(θ))2|\cos^2(\theta) - sin^2(\theta)| = \sqrt{( \cos^2(\theta) - sin^2(\theta) )^2}∣cos2(θ)−sin2(θ)∣=(cos2(θ)−sin2(θ))2
Ce n'est peut être pas ce que le prof attend ... cependant, cela répond entièrement à l'énoncé posé.
-
medou coulibaly dernière édition par

@Black-Jack Bonjour monsieur, je ne comprends pas bien votre méthode
-
2cos2(x)−1=2(cos2(x)−12)2cos^2(x)-1= 2(cos^2(x)-\dfrac{1}{2})2cos2(x)−1=2(cos2(x)−21)
en utilisant une identité remarquable :
....
-
medou coulibaly dernière édition par

@Noemi Bonsoir je pense que
2cos^2(θ) -1 factorisé est : 2(cos^2θ -1/2)
-
Tu peux factoriser le terme entre parenthèses.
-
medou coulibaly dernière édition par

@Noemi je trouve ( cos(θ) - 1 )(cos(θ) + 1 )
-
BBlack-Jack dernière édition par
@medou-coulibaly a dit dans Ecrire sans les valeurs absolues :
@Black-Jack Bonjour monsieur, je ne comprends pas bien votre méthode
Bonjour,
Méthode évidente.
Soit f(x) une fonction qui peut être aussi bien positive que négative.
|f(x)| = f(x) pour les valeurs de x telles que f(x) >= 0
|f(x)| = -f(x) pour les valeurs de x telles que f(x) <= 0Donc : |f(x)|² = (f(x))² >= 0 pour tout x du domaine de définition.
--> ∣f(x)∣=(f(x))2|f(x)| = \sqrt{(f(x))^2}∣f(x)∣=(f(x))2 ... quelle que soit f(x)
La relation donnée dans mon message précédent est correcte pour toutes valeurs de x et donc aussi sur ]-Pi ; Pi[
Le membre de droite est bien écrit sans utilisation de valeurs absolues ... et est égal au membre de gauche. Cette relation répond donc parfaitement à l'énoncé.
Qu'est ce que tu ne comprends pas la dedans ?
Un exemple simpliste :
Soit g(x) = |x| pour x dans R
Ecrire g(x) sans les valeurs absolues ...Ma réponse donne alors : g(x)=x2g(x) = \sqrt{x^2}g(x)=x2 ... qui est bien g(x) écrit sans utiliser des valeurs absolues.
Et on a bien ∣x∣=x2|x| = \sqrt{x^2}∣x∣=x2 sur R
C'est évident ...
C'est cette même "méthode" qui a été utilisée avec ma réponse initiale.
'''''''''''''''''''''''Je ne sais pas si c'est cela qui est attendu par ton prof ... mais cette façon de faire répond exactement à l'énoncé tel qu'il est posé.
-
medou coulibaly dernière édition par

@Noemi j'ai du mal à faire mon tableau de signe car mes valeurs ne tombent pas sur ce que je recherche
-
medou coulibaly dernière édition par

@Black-Jack je suis là lire votre message je vais vous revenir
-
(cos(θ)−1)(cos(θ)+1)=cos2(θ)−1(cos(\theta)-1)(cos(\theta)+1)= cos^2(\theta)-1(cos(θ)−1)(cos(θ)+1)=cos2(θ)−1
et non à cos2(θ)−12cos^2(\theta)-\dfrac{1}{2}cos2(θ)−21cos2(θ)−12=(cos(θ)−22)(cos(θ)+22)cos^2(\theta)-\dfrac{1}{2}=(cos(\theta)-\dfrac{\sqrt2}{2})(cos(\theta)+\dfrac{\sqrt2}{2})cos2(θ)−21=(cos(θ)−22)(cos(θ)+22)
-
medou coulibaly dernière édition par

@Noemi ok (cos θ - √2/2)(cosθ + √2/2 ) = 0
cos θ - √2/2 = 0 ou cosθ + √2/2 = 0
cos θ = √2/2 ou cosθ = - √2/2
-
Résous ces équations et fait un tableau de signes.
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Ne pas lire avant d'avoir complété la piste donnée par Noemi.
f(x)=∣cos2(x)−sin2(x)∣=∣cos(2x)∣f(x) = |cos^2(x) - sin^2(x)| = |cos(2x)|f(x)=∣cos2(x)−sin2(x)∣=∣cos(2x)∣ sur [-Pi ; Pi]
cos(2x) >= 0 pour x dans [-Pi/2 ; Pi/2] mod (2Pi)
Donc : cos(2x) >= 0 pour x dans [-Pi/4 ; Pi/4] mod (Pi)D'où on tire directement :
cos(2x) >= 0 pour x compris dans [−π;−3π4]U[−π4;π4]U[3π4;π][-\pi ; -\frac{3\pi}{4}] U [-\frac{\pi}{4} ; \frac{\pi}{4}] U [\frac{3\pi}{4} ; \pi][−π;−43π]U[−4π;4π]U[43π;π]cos(2x) <= 0 pour x compris dans [−3π4;−π4]U[π4;3π4][-\frac{3\pi}{4} ; -\frac{\pi}{4}] U [\frac{\pi}{4} ; \frac{3\pi}{4}][−43π;−4π]U[4π;43π]
Une écriture possible de f(x) est :
f(x) = cos(2x) pour x compris dans [−π;−3π4] U [−π4;π4] U [3π4;π][-\pi ; -\frac{3\pi}{4}]\ U\ [-\frac{\pi}{4} ; \frac{\pi}{4}]\ U\ [\frac{3\pi}{4} ; \pi][−π;−43π] U [−4π;4π] U [43π;π]
f(x) = -cos(2x) pour x compris dans ]−3π4;−π4[ U ]π4;3π4[]-\frac{3\pi}{4} ; -\frac{\pi}{4}[\ U\ ]\frac{\pi}{4} ; \frac{3\pi}{4}[]−43π;−4π[ U ]4π;43π[Et on remarquera, en passant, qu'écrire f(x)=cos2(2x)f(x) = \sqrt{cos^2(2x)}f(x)=cos2(2x) ... sans avoir besoin de précision sur le domaine, répond à la question telle que posée dans l'énoncé.
-
medou coulibaly dernière édition par

@Noemi Bonjour
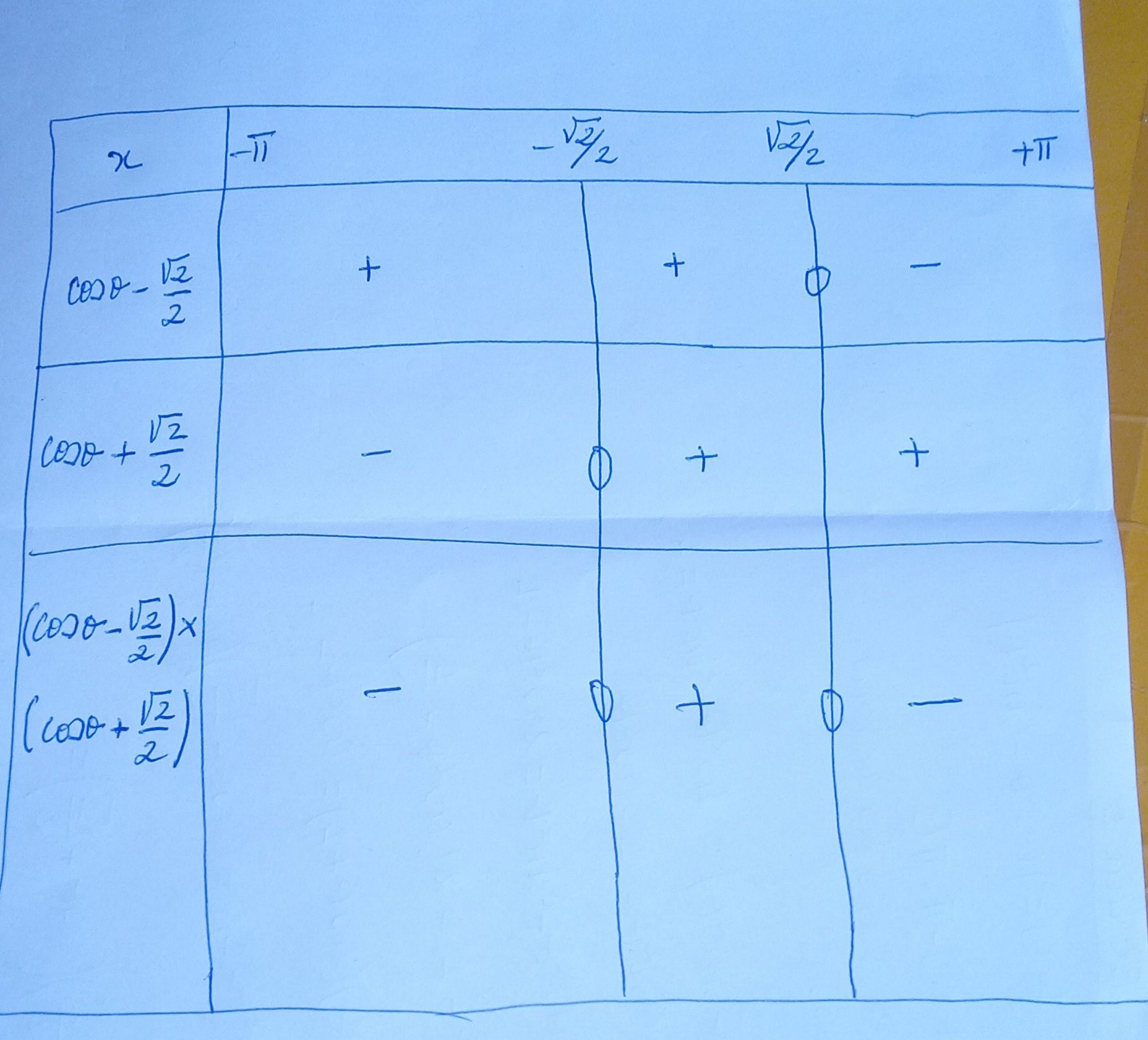 vérifier mon tableau de signe
vérifier mon tableau de signe
-
medou coulibaly dernière édition par medou coulibaly

@Black-Jack Bonjour j'ai lu votre message et j'ai vu le théorème dans mon livre de seconde
-
Tableau de signes à revoir.
Regarde ce cours : https://www.maths-et-tiques.fr/telech/TrigoTS.pdf
-
mtschoon dernière édition par mtschoon

Bonjour tout le monde,
@medou-coulibaly , le tableau que tu proposes (sur fond bleu) est à revoir.
Tu confonds θ\thetaθ avec cosθ\cos\thetacosθSur la ligne horizontale supérieure , ce sont des valeurs de θ\thetaθ qui doivent être indiquées (mets θ\thetaθ au lieu de xxx), non des valeurs de cosθcos\thetacosθ
Tu dois chercher les valeurs de θ\thetaθ, comprises entre -π\piπ et π\piπ, telles que cosθ−22=0cos\theta-\dfrac{\sqrt 2}{2}=0cosθ−22=0 et celles telles que cosθ+22=0cos\theta+\dfrac{\sqrt 2}{2}=0cosθ+22=0
Ce sont ces valeurs qui doivent être indiquées sur la ligne horizontale supérieure relative à θ\thetaθEnsuite, bien sûr, il faut trouver les signes exacts à mettre dans les cases
-
mtschoon dernière édition par

Si ça peut t'aider, je te poins le cercle trigonométrique qu'il faudra compléter avec les angles correspondants aux points C,D,E
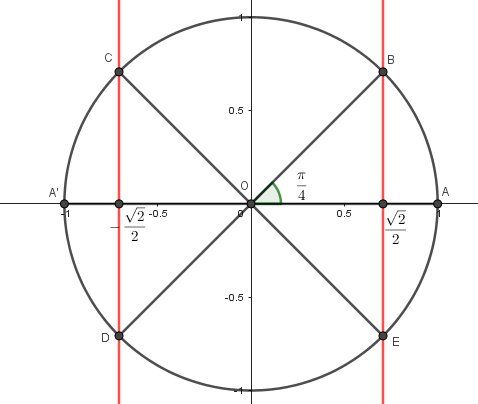
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame je mélange dans cet exercice c'est quoi vous voulez dire par là, la valeur de cosinus ?
-
medou coulibaly dernière édition par

@mtschoon oui je maîtrise un peu bien le cercle trigonométrie .
cosθ-√2/2 = 0 <==> cosθ = √2/2 ???
Là je bloque
mais je sais que cosθ =√2/2 <==> cosθ =cos π/4 donc je avoir θ = π/4
je bloque vraiment .....
-
As-tu regardé le lien que j'ai indiqué ?
-
mtschoon dernière édition par mtschoon

Regarde le lien donné par @Noemi
Tu peux aussi regarder le cercle trigonométrique que je t'ai dessiné.
Pour cosθ=22cos\theta=\dfrac{\sqrt 2}{2}cosθ=22, il ya deux points associés sur le cercle trigonométrique .
Il y a BBB qui correspond à l'angle dont une mesure est θ=π4\theta=\dfrac{\pi}{4}θ=4π
Il y a aussi le point EEE .
Indique la valeur d'angle θ\thetaθ correspondante (comprise entre −π-\pi−π et π\piπ)Pour cosθ=−22cos\theta=-\dfrac{\sqrt 2}{2}cosθ=−22, il ya deux points associés sur le cercle trigonométrique .
Ce sont les points CCC et DDD
Trouve les valeurs de θ\theta θ associées ( toujours comprises entre −π-\pi−π et π\piπ )Bien sûr, ce serait plus rapide de te les donner, mais cela ne te servirait à rien si ce n'est pas toi qui les trouve...
-
medou coulibaly dernière édition par

@Noemi je vais consulter
-
medou coulibaly dernière édition par

@mtschoon
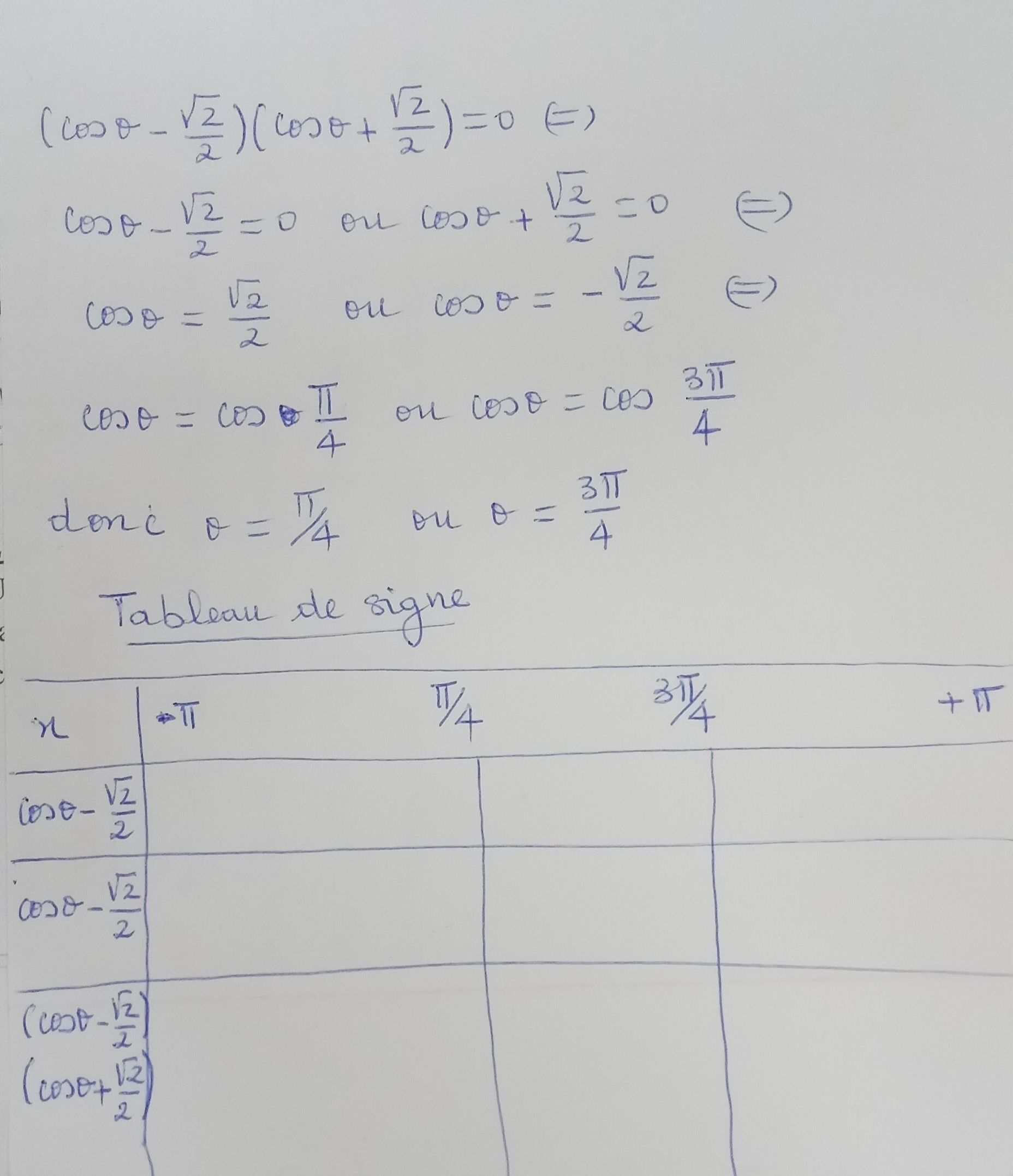 mes valeurs ne tombent pas lorsque je remplace θ par sa valeur
mes valeurs ne tombent pas lorsque je remplace θ par sa valeur
-
Regarde cette vidéo : https://www.youtube.com/watch?v=NIz3o4jKZnM
et ce cours : https://www.kartable.fr/ressources/mathematiques/methode/resoudre-une-equation-trigonometrique-du-type-cos-x-a/3519
-
mtschoon dernière édition par

Tu as sur le cercle trigonométrique quatre points A,B,C,D qui conviennent. (si tu as compris le cercle trigonométrique)
Donc dans ton tableau de signes , tu dois avoir quatre valeurs de θ\thetaθ sur la ligne horizontale supérieure.Tu en as écris deux θ=π4\theta=\dfrac{\pi}{4}θ=4π et θ=3π4\theta=\dfrac{3\pi}{4}θ=43π qui correspondent aux points B et C
Elles conviennent (forcément !):
cosπ4=22cos\dfrac{\pi}{4}=\dfrac{\sqrt 2}{2}cos4π=22 <=> cosπ4−22=0cos\dfrac{\pi}{4}-\dfrac{\sqrt 2}{2}=0cos4π−22=0
cos3π4=−22cos\dfrac{3\pi}{4}=-\dfrac{\sqrt 2}{2}cos43π=−22 <=> cos3π4+22=0cos\dfrac{3\pi}{4}+\dfrac{\sqrt 2}{2}=0cos43π+22=0Il te reste à donner les valeurs de θ\thetaθ (toujours entre −π-\pi−π et π\piπ) qui correspondent aux points D et E
-
medou coulibaly dernière édition par

@mtschoon les valeurs de θ moi je comprends pas cela
-
mtschoon dernière édition par mtschoon

Bonjour,
@medou-coulibaly , ta difficulté c'est que tu ne sembles pas avoir les bases de trigonométrie de lycée , première en principe (fonctionnement des mesures des angles orientés en radians, positionnement sur le cercle trigonométrique, cosinus, sinus,...)Si tu as encore tes cours de lycée, essaie de les consulter, car les liens proposés ne semblent pas te servir.
Lorsque j'aurais un peu de temps, j'essaierai de t'expliciter un peu l'usage du cercle trigonométrique (mais on ne peut pas faire un cours détaillé sur un forum...)
Bon courage !
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame , j'ai compris.
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , tu as compris quoi?
Merci de l'indiquer.A tout hasard je te mets un lien sur l'utilisation du cercle trigonométrique. Consulte le vraiment.
https://www.youtube.com/watch?v=ECNX9hnhG9UEnsuite, indique ( si tu y arrives) les deux valeurs manquantes pour θ\thetaθ dans ton tableau de signes.
Rappel : Dans ton exercice, la variable ne s'appelle pas xxx, elle s'appelle θ\thetaθ
-
medou coulibaly dernière édition par

@mtschoon ok merci beaucoup madame je vais pour revenir dessus, j'ai posté un DM que je bloque dessus
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , bonsoir,
Je te conseille de la rigueur pour progresser.
Tu devrais approfondir les bases de la trigonométrie (consulter la video proposée sur le cercle trigonométrique) et terminer cet exercice avant d'en commencer un autre.
Propose au moins les 4 valeurs de θ\thetaθ ( mesures principles des angles ) que tu dois mettre dans le tableau de signes
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame , j'ai compris.L'autre exercice est un DM à déposer le mardi donc , j'ai du le posté vu que je rencontre des difficultés dessus
-
mtschoon dernière édition par

@medou-coulibaly , bonjour,
Je ne sais pas trop ce que tu as compris...
Je te mets le cercle trigonométrique complété avec les valeurs particulières nécessaires.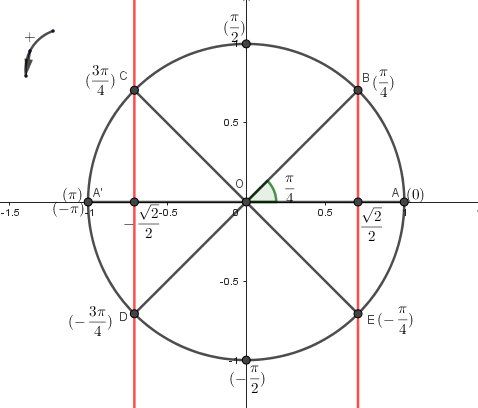
-
mtschoon dernière édition par mtschoon

je te mets le tabeau de signes, que tu dois trouver.
Ensuite, suivant le signes de l'expression cos2θ−12cos^2\theta-\dfrac{1}{2}cos2θ−21 , il te reste à donner les écritures simplifiées (sans symboles de valeurs absolues) de ∣cos2θ−12∣|cos^2\theta-\dfrac{1}{2}|∣cos2θ−21∣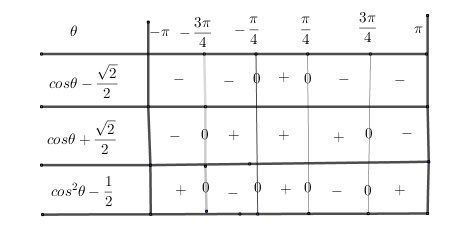
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame j'ai compris merci
Maintenant je dois remplacer les valeurs de cos^2θ + sin^2θ ?
c'est à dire je dois calculer avec une machine ?
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , bonjour,
@medou-coulibaly a dit dans Ecrire sans les valeurs absolues :
@mtschoon Bonjour madame j'ai compris merci
Maintenant je dois remplacer les valeurs de cos^2θ + sin^2θ ?
c'est à dire je dois calculer avec une machine ?Je ne comprends pas de quoi tu parles....
Je te rappelle que cos2θ−sin2θ=2cos2θ−1cos^2\theta-sin^2\theta=2cos^2\theta-1cos2θ−sin2θ=2cos2θ−1
1er cas :
Pour θ∈]−π,−3π4]∪[−π4,π4]∪[3π4,π[\boxed{\theta \in ]-\pi,-\dfrac{3\pi}{4}]\cup [-\dfrac{\pi}{4},\dfrac{\pi}{4}]\cup [\dfrac{3\pi}{4},\pi[}θ∈]−π,−43π]∪[−4π,4π]∪[43π,π[, l'expression 2cos2θ−12cos^2\theta-12cos2θ−1 est positive donc :∣cos2θ−sin2θ∣=∣2cos2θ−1∣=cos2θ−sin2θ=2cos2θ−1|cos^2\theta-sin^2\theta|=|2cos^2\theta-1|=\boxed{cos^2\theta-sin^2\theta}=\boxed{2cos^2\theta-1}∣cos2θ−sin2θ∣=∣2cos2θ−1∣=cos2θ−sin2θ=2cos2θ−1
2ème cas :
Pour θ∈]−3π4,−π4]∪[π4,3π4]\boxed{\theta\in ]-\dfrac{3\pi}{4},-\dfrac{\pi}{4}]\cup[\dfrac{\pi}{4},\dfrac{3\pi}{4}]}θ∈]−43π,−4π]∪[4π,43π] , l'expression 2cos2θ−12cos^2\theta-12cos2θ−1 est négative donc :∣cos2θ−sin2θ∣=∣2cos2θ−1∣=−(cos2θ−sin2θ)=−(2cos2θ−1)|cos^2\theta-sin^2\theta|=|2cos^2\theta-1|=-(cos^2\theta-sin^2\theta)=-(2cos^2\theta-1)∣cos2θ−sin2θ∣=∣2cos2θ−1∣=−(cos2θ−sin2θ)=−(2cos2θ−1)
c'est à dire :
∣cos2θ−sin2θ∣=∣2cos2θ−1∣=−cos2θ+sin2θ|cos^2\theta-sin^2\theta|=|2cos^2\theta-1|=\boxed{-cos^2\theta+sin^2\theta } ∣cos2θ−sin2θ∣=∣2cos2θ−1∣=−cos2θ+sin2θ=−2cos2θ+1\boxed{-2cos^2\theta+1}−2cos2θ+1
-
medou coulibaly dernière édition par

@mtschoon J'ai compris je vais bien reprendre
-
mtschoon dernière édition par

-
medou coulibaly dernière édition par

@mtschoon Bonsoir Madame jai repris et cest juste.
-
mtschoon dernière édition par

C'est très bien @medou-coulibaly