Fonctionnement f de x
-
MMMounah dernière édition par
Bonsoir
f(x)=tan(x2)cos(2x)f(x)=tan(\frac{x}{2})cos(2x)f(x)=tan(2x)cos(2x)
Cette fonction est paire ou impaire . Quel interval d’étude choisir ??
-
mtschoon dernière édition par

@Zeïnab-Mahamadou , bonjour,
Je te donne des indications mais elles doivent être justifiées.
i) La fonction xxx-> cos(2x)cos(2x)cos(2x) est paire
La fonction xxx-> tan(x2)tan(\dfrac{x}{2}) tan(2x) est impairedonc la fonction fff est impaire (produit d'une fonction paire par une fonction impaire)
ii) ) La fonction xxx-> cos(2x)cos(2x)cos(2x) a pour période π\piπ
La fonction xxx-> tan(x2)tan(\dfrac{x}{2}) tan(2x) a pour période 2π2\pi2πdonc la fonction fff a pour période 2π2\pi2π
Tu peux étudier fff sur l'intervalle [0,π][0,\pi][0,π]
Avec l'imparité, tu obtiendras fff sur [−π,0][-\pi,0][−π,0]
Ainsi, tu connaîtras fff sur [−π,π[-\pi,\pi[−π,π], c'est-à-dire sur une période.La connaissance de fff se complète par périodicité de période 2π2\pi2π
-
mtschoon dernière édition par

@Zeïnab-Mahamadou
Illustration graphique de fff
(les droites en pointillés rouge sont asymptotes à la représentation graphique de fff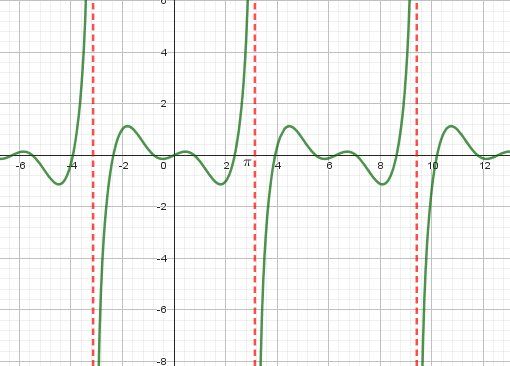
-
MMMounah dernière édition par MMounah
@mtschoon bonsoir
Merci madame
ii) mais si x—>cos(2x) est π\piπ Période et x—>tan(x/2) est 2π\piπ Pourquoi f(x)=tan(x/2)cos(2x)f(x)=tan(x/2)cos(2x)f(x)=tan(x/2)cos(2x) est 2π\piπ
-
mtschoon dernière édition par mtschoon

@Zeïnab-Mahamadou ,
Réponse relative à ii) :
parce la période doit être le plus petit commun multiple des deux périodes, c'est à dire ici 2π2\pi2π
-
MMMounah dernière édition par
@mtschoon je pense avoir compris merci
-
mtschoon dernière édition par

De rien @Zeïnab-Mahamadou
Reposte si besoin.