Problème de produit scalaire

[Christophe Christophe]

Bonjour à tous,

voici un problème de produit scalaire que je n'arrive pas à finaliser ...

Enoncé
))

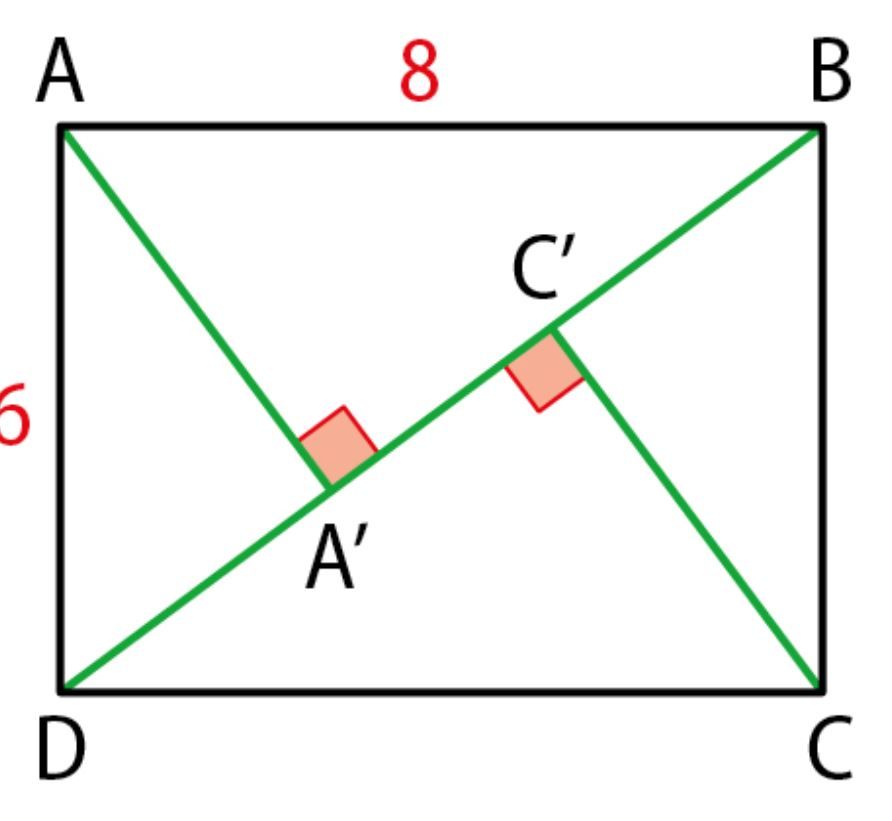
Un rectangle ABCD avec $AB=8$, $AC=6$, A' projeté orthogonal de A sur BD et C' projeté orthogonal de C sur BD.

1. Décomposer $\overrightarrow{AC}$ en faisant apparaitre ${\overrightarrow{A^{\prime }C}}^{\prime }$
   2.a Montrer que $\overrightarrow{AC}.\overrightarrow{BD}=\overrightarrow{A^{\prime }{C}^{\prime }}.\overrightarrow{BD}$
   2b. Montrer que $AD²-AB²=\overrightarrow{AC}.\overrightarrow{BD}$
2. Déduire des questions précédentes A'C'.

Mon travail

Pas de problème pour les question 1 et 2a... Par contre je sèche sur la 2b ....
$AD²-AB²=-28$ mais montrer que celà est = à $\overrightarrow{AC}.\overrightarrow{BD}$ là j'ai beau chercher je ne vois pas ...
Pourriez-vous me donner un indice afin de me permettre d'avancer sur ce poroblème svp ?
Je vous en remercie par avance

[Black-Jack]

Bonjour,

2b

$\overrightarrow{AC}.\overrightarrow{BD}$

$=(\overrightarrow{AD}+\overrightarrow{DC}).(\overrightarrow{BA}+\overrightarrow{AD})$

$=(\overrightarrow{AD}+\overrightarrow{DC}).(\overrightarrow{CD}+\overrightarrow{AD})$

$=\overrightarrow{AD}.\overrightarrow{CD}+\overrightarrow{AD}.\overrightarrow{AD}+\overrightarrow{DC}.\overrightarrow{CD}+\overrightarrow{DC}.\overrightarrow{AD}$

$=A{D}^2+\overrightarrow{AD}.(\overrightarrow{CD}+\overrightarrow{DC})-D{C}^2$

$=A{D}^2-D{C}^2$

$=A{D}^2-A{B}^2$

Il y a probablement un rien plus direct.

[Christophe Christophe]

Un très grand merci @Black-Jack... Et une fois de plus j'éprouve une grande honte