tableau de signe de la fonction dérivée

Bonjour, je n'arrive pas à dresser le tableau de signe de f'(x) sachant que
$\frac{5e^{-2x^2}}{2-|x|}$ .
Je ne trouve pas toutes les racines de f'(x) car j'ai calculé la dérivée en supposant que x>0 et donc que |x|=x. Je ne comprends pas comment trouver les autres racines.

Bonjour,

Si x >= 0, $\frac{5.e^{-2x^2}}{2-x}$
Si x < 0, $\frac{5.e^{-2x^2}}{2+x}$

Tu peux donc chercher les dérivées en séparant les cas x >= 0 et x < 0

Attention que f n'existe pas pour x = -2 ou x = 2

Bonjour,

@lala-o , si tu veux te simplifier le travail, tu peux utiliser la parité de f.

Pour tout $\in R\$ \ {-2,2} ,
$f (- x) = f (x)$ car $x)^2=x^2$ et $∣ - x ∣ = ∣ x ∣$
donc $f$ paire.

Tu peux donc travailler seulement pour $x$ positif et déduire sans calculs, par parité, pour $x$ négatif ( et graphique symétrique par rapport à l'axe des ordonnées).

@lala-o ,

Je viens de calculer la dérivée pour x positif privé de 2 .

Sauf erreur :
$f(x)=1+5e−2x22−xf(x)=1+\dfrac{5e^ {-2x^2}}{2-x}$

$f′(x)=5(4x2−8x+1)e−2x2(2−x)2f'(x)=\dfrac{5(4x^2-8x+1)e^{-2x^2}}{(2-x)^2}$

Vérifie.

Si c'est bien ça, le signe de $f^{'} (x)$ est le signe de $4x^2-8x+1)$ (pour x positif privé de 2)

Bons calculs.

@mtschoon Bonjour, j'obtiens la même chose pour x>0. Mais pour x<0, j'obtiens $4x^2-8x+1$ dans le numérateur de f'(x). Les racines ne sont donc pas l'opposé de celles de f'(x) pour x>0, alors que c'est le cas dans la réponse.

Aussi, je dois trouver un minimum en x=0. Je ne vois pas d'où il pourrait venir.

@lala-o ,

Comme déjà dit, si tu connais, utiliser la parité permet de trouver le signe le la fonction dérivée sans calcul pour x négatif, en connaissant le signe de la dérivée pour x positif.

Si tu fais le calcul pour $x$ négatif, tu dois trouver, sauf erreur,
$f′(x)=5(−4x2−8x−1)e−2x2x+2)2f'(x)=\dfrac{5(-4x^2-8x-1)e^{-2x^2}}{x+2)^2}$

Pour $x$ positif, la dérivée s'annule pour $x=2+32x=\dfrac{2+\sqrt 3}{2}$ et pour $x=2−32x=\dfrac{2-\sqrt 3}{2}$

Pour $x$ négatif, la dérivée s'annule pour $x=−2−32x=\dfrac{-2-\sqrt 3}{2}$ et pour $x=−2+32x=\dfrac{-2+\sqrt 3}{2}$ , ce qui est évident pour raison de parité.

Ah oui, j'ai fais une erreur de signe. Mais je ne comprends toujours pas comment déterminer ce qu'il se passe en x=0? Pourquoi 0 n'apparait il pas dans les racines de f'(x) si c'est un extremum?

@lala-o a dit dans tableau de signe de la fonction dérivée :

Aussi, je dois trouver un minimum en x=0. Je ne vois pas d'où il pourrait venir.

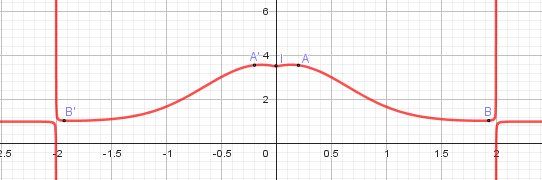
Si tu cherches soigneusement le sens de variation de $f$ , tu trouveras effectivement un minimum local pour $x = 0$ Point $I (0, 3.5)$ sur la courbe.
Cela ne correspond pas à une valeur qui annule la dérivée.
C'est seulement le point de la courbe qui est sur l'axe des ordonnées (axe de symétrie)
$f$ est croissante sur $[0,2−32]\biggr[0,\dfrac{2-\sqrt 3}{2}\biggr]$ (du point I au point A)
$f$ est décroissante sur $[−2+32,0]\biggr[\dfrac{-2+\sqrt 3}{2},0\biggr]$ (du point A' au point I)

Je te mets un schéma approximatif pour t'éclairer et te permet de vérifier, mais si j'ai bien compris ta question, il n'est pas à faire.
Je pense que tu dois faire seulement le tableau de variation.