Nombre complexe application

[MMounah]

Bonsoir
On identifie P plan complexe
$m(x;y)$ dans $R$ , on associe son affixe $z=x+iy$
a) Déterminer x et y fonction de z et son conjugué $zbar$
b) soit $f:\mathbb{C}$—>$\mathbb{C}$
Qui z fait correspondre affixe du point M=T(m) dans le repère R
Montrer que Z= iz + (1+i)zbar

[mtschoon]

@Zeïnab-Mahamadou , bonjour,

Pour la question a)
$z=x+iy$
$\bar{z}=x-iy$

En ajoutant membre à membre et en simplifiant , tu obtiens $x=\frac{z+\bar{z}}{2}$

En retranchant membre à membre et en simplifiant , tu obtiens $y=\frac{z-\bar{z}}{2i}$

Pour la b) , je ne vois pas qui est T(m), plus précisement , qu'est ce que T ?

Merci de préciser.

[MMounah]

@mtschoon bonsoir
Plus haut dans l’exercice l’énoncé parle de l’application T la translation de vecteur u mais dans la question ils n’ont pas précisé .
Si T est cette translation ça a un sens ??

[MMounah]

@mtschoon merci pour première question
Au faite c’est la deuxième partie de l’exercice (il est très long l’exercice).Et Je pense que les deux partie ne sont pas indépendantes .
Je vais essayer de traiter l’exercice dès le début

[mtschoon]

@Zeïnab-Mahamadou , bonsoir,

La forme complexe d'une translation de vecteur $\overrightarrow{U}$ de coordonnées $(a,b)$ est : $z^{\prime }=z+(a+ib)$.

Il faut écrire l'énoncé tel qui t'a été donné, si tu as besoin d'aide.

[mtschoon]

@Zeïnab-Mahamadou , bonjour,

Comme indiqué, T ne peut pas être une translation, vu que la forme que tu donnes $z^{\prime }=iz+(1+i)\bar{z}$ ne correspond pas à la forme complexe d'une translation.

T veut peut-être dire Transformation.

Je peux te dire, si cela t'est utile, que $z^{\prime }=iz+(1+i)\bar{z}$ est la forme complexe de la symétrie axiale, d'axe (d) d'équation $y=x$ et de direction l'axes des ordonnées (axe des imaginaires).

Preuve :
Si l'on fait les calculs :
soit $z=x+iy$ et $z^{\prime }=x^{\prime }+i{y}^{\prime }$(je mets $z^{\prime }$ au lieu de $Z$ pour éviter les confusion dans les notations)

$z^{\prime }=iz+(1+i)\bar{z}$ <=> $x^{\prime }+i{y}^{\prime }=i(x+iy)+(1+i)(x-iy)$
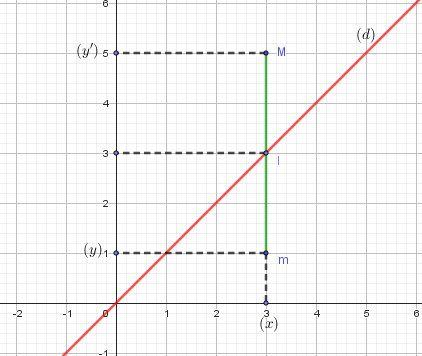
c'est à dire, après calculs : $x^{\prime }=x$ et $y^{\prime }=2x-y$

Recherche des points invariants : $z^{\prime }=z$ tu dois trouver $\boxed{y=x}$ (droite (d) ).

Soit $m(x,y)$ et $M(x^{\prime },y^{\prime })$ et $I(x,x)$ de la droite (d)

$\overrightarrow{Im}$ a pour coordonnées $(x-x,y-x)$ c'est à dire $(0,y-x)$
$\overrightarrow{IM}$ a pour coordonnées $(x-x,y^{\prime }-x)$ c'est à dire $(0,y^{\prime }-x)$
Vu que $y^{\prime }=2x-y$, tu obtiens :
$\overrightarrow{IM}$ a pour coordonnées $(0,x-y)$

Donc : $\boxed{\overrightarrow{IM}=-\overrightarrow{Im}}$

Conclusions :
(mM) parallèle à l'axe des ordonnées
I milieu de [mM]

Donc la nature de T que je t'ai proposée.

Evidemment, suivant ton énoncé, il faut faire les calculs dans l'autre sens : partir de T que tu devrais connaître (? ? ? ) et trouver sa forme complexe.

[mtschoon]

illustration graphique