Vérifier si l'ensemble est un espace vectoriel
-
-lala-o dernière édition par

Bonjour, j'aimerais avoir une correction pour cet exercice :
Vérifier si l'ensemble est un espace vectoriel : E={(x,y)ϵR2\epsilon R^2ϵR2 | sin(x+y)=0}
Voilà ma résolution :
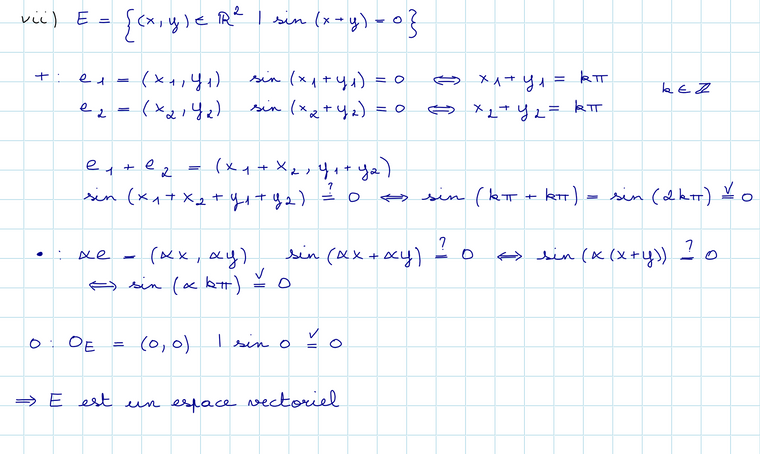
-
mtschoon dernière édition par mtschoon

@lala-o , bonsoir,
Je pense que ta question est de savoir si EEE est un SEV de R2R^2R2
Cela me semble correct.
-
-lala-o dernière édition par

@mtschoon Bonjour, je viens de vérifier dans mon cours et il m'est bien demandé de montrer si ce sont des espaces vectoriels, non pas des sous espaces vectoriels.
-
mtschoon dernière édition par mtschoon

@lala-o , bonjour,
Sans te le dire, ton cours, pour simplifier, doit considérer que R2R^2R2, muni des operations usuelles, est un espace vectoriel (ça a dû être démontré en cours), et te demande démontrer que EEE est un sous espace-vectoriel de R2R^2R2
Je te mets un lien sur la définition de sous-espace vectoriel
https://www.bibmath.net/dico/index.php?action=affiche&quoi=./s/sev.htmlSi tu voulais démontrer avec rigueur que EEE est un espace vectoriel, il faudrait faire beaucoup plus de travail ! :
Regarde ici la définition exacte d'un espace vectoriel
https://www.imo.universite-paris-saclay.fr/~michel.rumin/enseignement/S2PMCP/3-Espaces vectoriels.pdfIl faudrait que tu prouves toutes les propriétés de la loi interne (addition) et de la loi externe (multiplication par un réel)...
Utilise donc, sans soucis, la simplification de ton cours ( bien que j'aurais préféré que l'énoncé te dise de prouver que EEE est un sous-espace vectoriel de R2R^2R2, ce qui aurait été plus correct )
-
-lala-o dernière édition par

@mtschoon Je pense que le but de l'exercice est bien de montrer que c'est un espace vectoriel et pas un sous espace vectoriel. Dans ce cas, est ce que ma résolution est-elle toujours correcte? Si l'on prouve que E est un sous espace vectoriel, E est forcément un espace vectoriel, non? Voilà une photo de l'exercice complet (l'exercice demandé est la sous question vii)

-
mtschoon dernière édition par

@lala-o ,
En toute rigueur un sous-espace vectoriel, comme son nom l'indique, est un espace-vectoriel inclus dans un espace vectoriel.Quand on est dans un espace vectoriel (ici R2R^2R2), un sous-ensemble est un sous-espace vectoriel ( c'est à dire un espace vectoriel inclus dans R2R^2R2) s'il est non vide, stable pour l'addition et pour la multiplication par un scalaire.
Regarde les liens que je t'ai indiqués.
Donc, ta résolution est correcte.