Coniques fonctionssqsss

[MMounah]

5. soit r la rotation de centre o et d’angle (-pi/4)
   (T): 3($x^2+y^2)-2xy-16=0$
   On désigne par (T’) l’image de r par (T)
   a) déterminé une équation cartésienne de (T)
   b) construire (T) et (T’) dans le même repère

[mtschoon]

@Zeïnab-Mahamadou , bonjour,

Je pense qu'au a), tu cherches l'équation cartésienne de (T')

Piste en passant par les complexes.
$z^{\prime }=z{e}^{-i\frac{\pi }{4}}$

$x^{\prime }+i{y}^{\prime }=(x+iy)(cos\frac{\pi }{4}+i\frac{\pi }{4})$

$x^{\prime }+i{y}^{\prime }=(x+iy)(\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2})$

En développant et en identifiant les parties réelles entre elles et les parties imaginaires entre elles, après calculs, tu dois trouver, sauf erreur, :
$x^{\prime }=\frac{\sqrt{2}}{2}(x+y)$
$y^{\prime }=\frac{\sqrt{2}}{2}(-x+y)$

En ajoutant et en retranchant membre à membre égalités, tu obtiens :
$x=\frac{\sqrt{2}}{2}(x^{\prime }+y^{\prime })$

$y=\frac{\sqrt{2}}{2}(x^{\prime }-y^{\prime })$

En subsituant dans l'équation de départ, tu obtiens après calculs :

$\boxed{x^{\prime 2}+2y^{\prime 2}=8}$

En diviasans par $8$ ; tu peux écrire :

$\frac{x^{\prime 2}}{8}+\frac{y^{\prime 2}}{4}=1$
c'est à dire :
$\boxed{\frac{x^{\prime 2}}{(2\sqrt{2}{)}^2}+\frac{y^{\prime 2}}{2^2}=1}$

Tu reconnaîs ainsi l'équation usuelle d'une ellipse (T') que tu peux construire.

Ensuite, par rotation de centre $O$ et d''angle $+\frac{\pi }{4}$, tu peux déduire la construction de l'ellipse (T).

Bons calculs.

[mtschoon]

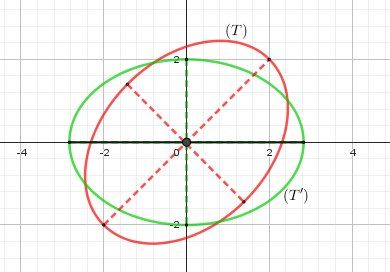
Illustration graphique

(T) est l'ellipse en rouge
(T') est l'ellipse en vert

[MMounah]

@mtschoon merci, c’est exact

[mtschoon]

De rien @Zeïnab-Mahamadou .
Je me doutais bien que tu avais fait une faute de frappe à la question a).

Cet exercice était intéressant.

Bon travail !