Lieux géométriques (synthétique)
-
-lala-o dernière édition par

Bonjour, j'aimerais de l'aide pour cet exercice :
"Recherche et construis le lieu du sommet d'un angle constant α\alphaα dont les côtés sont tangents respectivement à 2 cercles donnés de même centre O."
-
mtschoon dernière édition par mtschoon

@lala-o , bonjour,
Je te donne une idée possible mais il faudra détailler l'explication avec rigueur.
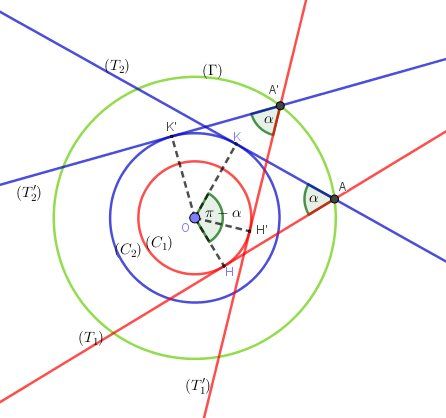
Notations:(C1)(C_1)(C1) et (C2)(C_2)(C2) deux cercles de centre OOO (un en rouge et l'autre en bleu sur le schéma)
(T1)(T_1)(T1) et (T2)(T_2)(T2) les tangentes qui se coupent en AAA telles que HAK^=α\widehat{HAK}=\alphaHAK=αAnalyse :
Rappel : la somme des angles d'un quadrilatère convexe vaut 2π2\pi2π radians
Les tangentes étant perpendiculaires aux rayons, dans le quadrilatère OHAKOHAKOHAK , vu que HAK^=α\widehat{HAK}=\alphaHAK=α, tu peux déduire après calculs, que nécessairement HOK^=π−α\widehat{HOK}=\pi-\alphaHOK=π−αSynthèse : construction d'un point AAA du lieu cherché
Tu prends un point quelconque HHH sur (C1)(C_1)(C1).
Tu places KKK sur (C2)(C_2)(C2) tel que HOK^=π−α\widehat{HOK}=\pi-\alphaHOK=π−α
Tu traces les tangentes (T1)(T_1)(T1) et (T2)(T_2)(T2)
Tu obtiens ainsi le point AAA, intersection de ces 2 tangentes tel que HAK^=α\widehat{HAK}=\alphaHAK=αTu as donc construit un point AAA du lieu cherché.
Conséquence :
Par toute rotation de centre 000, l'ensemble (T1),(T2),H,K,A)(T_1), (T_2), H,K, A)(T1),(T2),H,K,A), aura pour image l'ensemble (T1′),(T2′),H′,K′,A′)(T'_1), (T'_2), H',K', A')(T1′),(T2′),H′,K′,A′) tel que H′A′K′^=HAK^=α\widehat{H'A'K'}=\widehat{HAK}=\alphaH′A′K′=HAK=αLe lieu cherché sera le cercle (Γ)(\Gamma)(Γ) de centre OOO passant par AAA (en vert sur le schéma)
-
-lala-o dernière édition par

@mtschoon Bonsoir, merci pour votre explication. Pourriez vous également m'aider pour déterminer le rayon du cercle du lieu ?
-
mtschoon dernière édition par

@lala-o , bonsoir,
Vu que tu cherches une explication "synthétique" d'après ton titre, donc sans géométrie analytique dans un repère du plan, tu ne peux pas avoir une expression numérique du rayon.
AAA étant construit (voir la partie Synthèse), AAA est ainsi un point fixé, le lieu est le cercle (Γ)(\Gamma)(Γ) de centre OOO et de rayon OAOAOA
-
-lala-o dernière édition par

@mtschoon Bonjour, je ne comprends pas ce que je dois faire pour démontrer que le lieu est un cercle et que son rayon est OA.
-
mtschoon dernière édition par mtschoon

@lala-o ,
Idée :
Comme déjà indiqué, tu construis un point AAA du lieu cherché.
Les autres points du lieu se déduisent du point AAA en faisant des rotations de centre OOO
Pour toute valeur xxx , par rotation R(O,x)R(O,x)R(O,x) :
(T1)(T_1)(T1) a pour image (T1′)(T'_1)(T1′)
(T2)(T_2)(T2) a pour image (T2′)(T'_2)(T2′)
HHH a pour image H′H'H′
KKK a pour image K′K'K′
AAA a pour image A′A'A′Par rotation, les angles, les distances, sont conservées.
OA=OA′OA=OA'OA=OA′
H′OK′^=α\widehat{H'OK'}=\alphaH′OK′=αD'où la conclusion.
-
-lala-o dernière édition par -lala-o

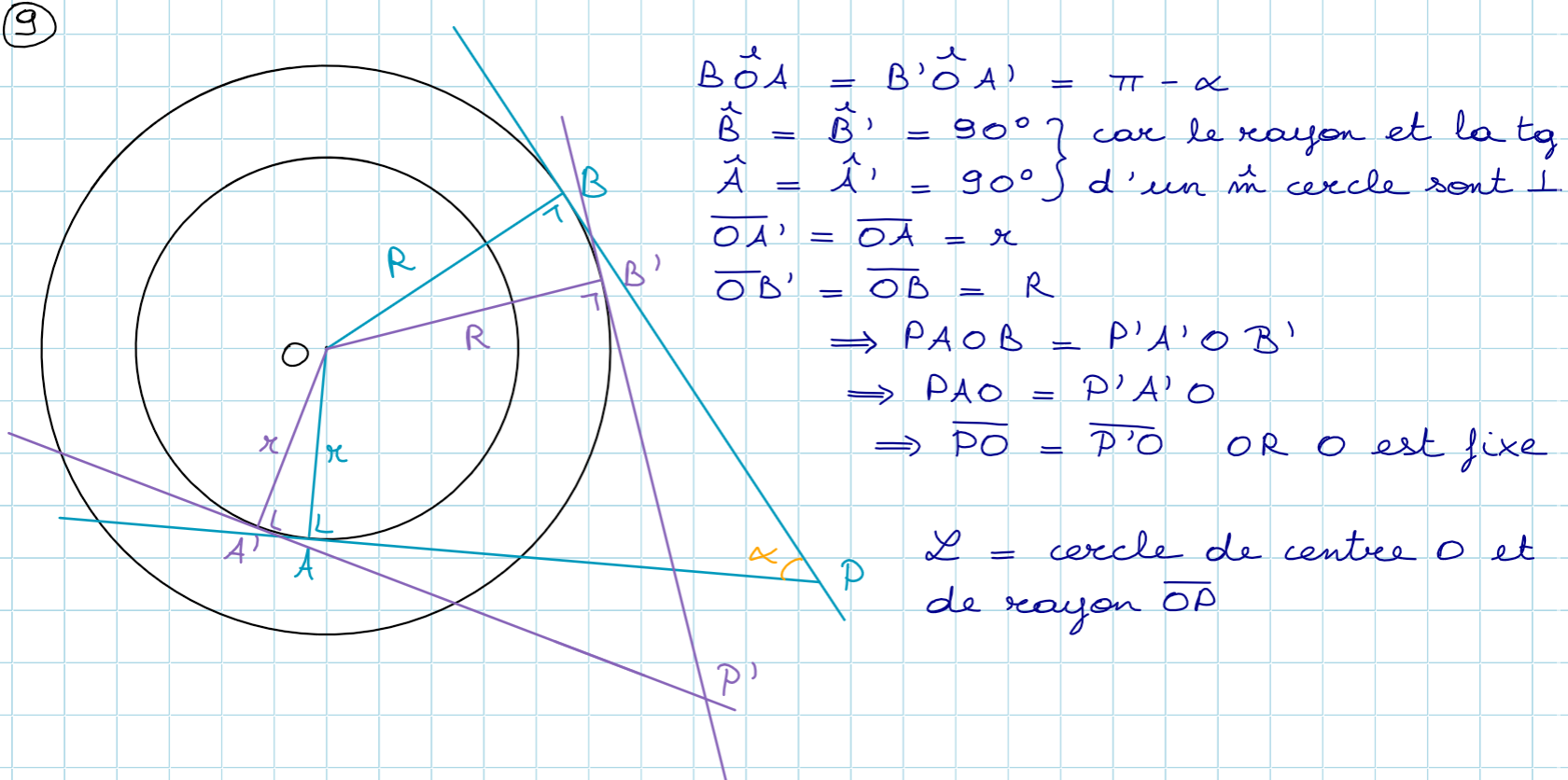
@mtschoon Bonjour, merci beaucoup pour vos réponses ! Voici ma résolution. Est-elle correcte?