Trouver le lieu de l'orthocentre

[-lala-o]

Bonjour, j'ai du mal avec cet exercice :
" Dans le cercle de centre O, on trace 2 diamètres perpendiculaires [AB] et [CD]. Un point mobile M se déplace sur sa circonférence. On trace la droite BM qui rencontre CD en F. Recherche et construis le lieu de l'orthocentre du triangle variable OMF."

[Black-Jack]

Bonjour :

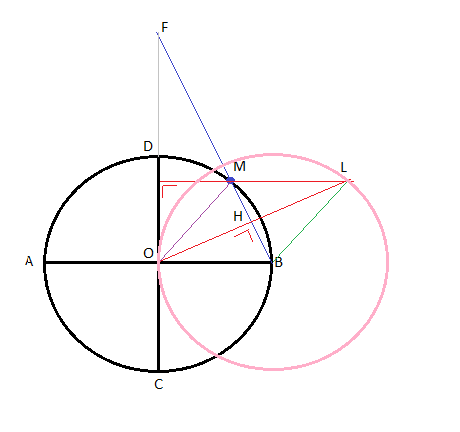
Soit L (voir dessin) un point du lieu cherché.

OH est la hauteur issue de 0 du triangle OMF
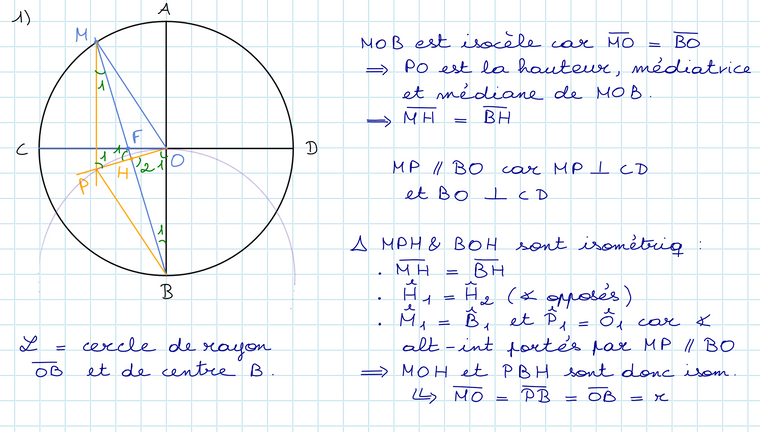
Comme OM = AB (rayons du cercle), le triangle MOB est isocèle en O ... et OH est à la fois hauteur, médiatrice (et médiane) du triangle MOB.

Les triangles OBH et LMH sont semblables (de même forme) car ils ont leurs angles égaux 2 à 2 (à expliquer)
Mais on a aussi MH=HB (puisque OH est aussi médiatrice de MB)
Et donc mles triangles OBH et LMH sont isométriques.
---> ML = OB
Or ML et OB sont parallèles comme perpendiculaires à une même droite (CD)

De ce qui précède, on déduit que le quadrilatère OBLM est un parallélogramme ... et donc que BL = OM
comme OM est un rayon R du cercle de diamètre AB (et CD), on a BL = R

Et donc le lieu de L est le cercle de centre B et de rayon R = BO, tracé en rose sur le dessin.

[-lala-o]

@Black-Jack Bonjour ! Merci beaucoup pour votre aide ! Pouvez-vous également vérifier si ma justification est suffisante ? Voilà ma résolution :